A kapcsolat a grafikon a funkció és a grafikon annak származékát - a problémák megoldását a kontroll

A kapcsolat a grafikon a funkció és a grafikon annak származéka

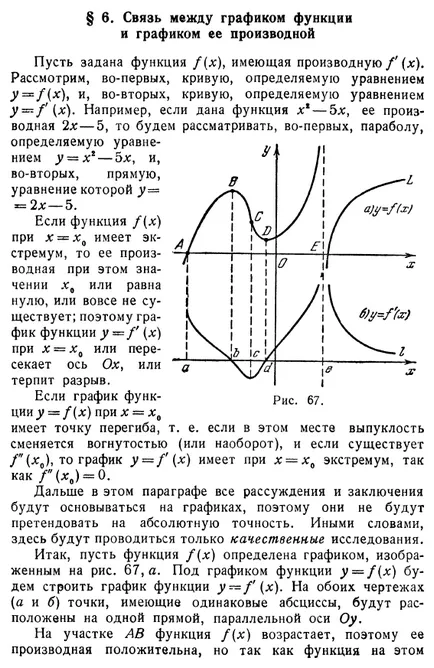
A kapcsolat a grafikon a funkció és a grafikon annak származéka Legyen egy f (x)> amelynek-származék / „(x). Tekintsük először, a görbe egyenlet által definiált y

/ (X), és, másodszor, a görbe által meghatározott y = zf (x). Például, ha egy adott funkció x * - 5ls, annak származéka 2-5, akkor meg fogja vizsgálni, először is, a parabola egyenlet által definiált y - x - ó, és, másodszor, egy egyenes vonal, amelynek egyenlet y = == 2 - 5. Ha a funkció / (x) x = x0 egy szélsőérték, annak származékát ezen az értéken x0 vagy nullára, vagy nem létezik; Ezért a grafikon y - f (x) x = x0 vagy x-tengely keresztezéssel vagy folytonossági hiány. Ha a gráf ábra G7 CIÓ függvény az y = f (x) az x = x0 egy inflexiós ponttal, azaz, ha ezen a ponton helyébe konvexitás konkáv (vagy fordítva), és van f „(x0), majd a grafikon y .. - f '

4) '8 (* + 2)' 3 3 és a § 3, III épült hsh- parabola y ^ = arg; jogal- március 3 látni, hogy az x-CH egy származéka (x-1x4-2) függvény v-V>. Ha összevetjük ezeket grafikus funkciókat a TIONS, megkapjuk a képet ábrán látható. 68. Ez a szám megerősíti a fenti. Gyakorlatok fejezet. VIII 1. Határozza meg a kritikus értéket, és fedezze fel a csökkenés és a növekedés xm függvény y = -16 x. 2. Határozza meg a kritikus értéket, és fedezze fel a növelés és csökkentés funkció # = X9 + ^ -x * + U 3. Határozza meg a kritikus értéket a függvény y - f *. 4. Határozza meg a kritikus értéket a függvény