A kötet a derékszögű paralelepipedon egyenlő 2,520 cm (egy kocka) és a bázis terület 168 cm (négyzet
Még rajz nem szükséges, mert megoldódott hangosan.
Szóval, mi az a mennyiség a dobozban? Vpar Sosn = * H, ahol H az egyik bordája, és minden 4. Itt a szám később.
Így találtunk egy éle. Ez maradt a másik két, amelyeket úgy kapunk, hogy bázisok.
Sosn = a * b; ahol a, b - a bázis oldalán a paralelepipedon.
Ismeretes, hogy a = b + 2
Így igaz ez:
A megoldás a másodfokú egyenlet, gyorsan és egyszerűen.
Válasz: b1 = 12; b2 = -14 (nem lehet olyan negatív)
Ennélfogva, b = 12; a = 12 + 2 = 14
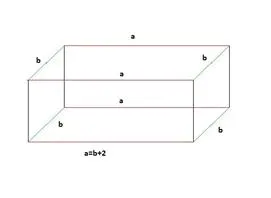
Az érthetőség kedvéért, én külön kijelölt él egy piros színű. Él b zöld, és a H magassága maradék tinta.
Kiderült, hogy csak egy téglatest 4 minden borda. Ez logikus, hogy írjon, hogy az összeg lesz egyenlő:
A területet a alapja a piramis egyenlő 108 dm 2, és a magassága - 24 dm. Szekcionált piramis bázis párhuzamos síkban van-nak 48 és 75 dm3. Keresse meg a távolságot a síkok a keresztmetszet.
Tehát van egy piramis ABCS (festett háromszögletű, mert ezt a feladatot, nincs különbség)
Szintén felhívni két részre DFE és D1F1E1 párhuzamos síkban ABC.
Most azt látjuk, hogy kap egy hasonló piramis. Nézzük meg a sorrendben:
1) Piramis DfES hasonló lesz a piramis ABCS. Szerint a szabály területek hasonlósági S (# 916; ABC) / S (# 916; DFE) = k2
Miután talált egy hasonlósági koefficiens találunk a magassága a piramis DfES.
108/48 = 2,25 → k = √ (2,25) = 1,5
Most ne feledjük, hogy a magassága a fél hasonló számadatok tekintetében megkapja k = h1 / h2
Tehát mi magassága egyenlő 24 / h (DfES) = 1,5 → h (DfES) = 24 / 1,5 = 16
2) Hasonlóképpen D1F1E1S piramis hasonló ABCS. Keressük a magassága, ugyanúgy.
24 / h (D1F1E1S) = 1,2 → h (D1F1E1S) = 24 / 1,2 = 20
3) Meg kell a távolság a síkban a DFE D1F1E1. Ez lesz egyenlő 20-16 = 4 dm.
A alapja a piramis - egy egyenlő szárú háromszög csúcsszöge # 945; és a sugara a körülírt kör R. A két egyenlőtlen oldalfelületei merőlegesek a alapsík és a harmadik arc ferde ahhoz szögben # 946;. Keresse oldalfelületén a piramis.
Az ábra azt mutatja, a piramis ABCS, a vertex S ave vedena apothem SK AC alján egy egyenlő szárú háromszög. Mindez azt kell megoldani ezt a problémát.
Így a kör sugara leírás megtalálható, mint:
R = a / 2sin # 945; → CB = a = R * 2sin # 945;
Most tudva oldalán CB talál másik oldalon az AC és AB, amely megegyezik egymással.
Nézzük írjuk le, amit területek képezik az oldalsó felület:
Most meg kell festeni, hogyan kell megtalálni mindegyik.
A szabályos háromoldalú piramis szegmens összekötő a bázis a középső magassága a piramis apothem, m jelentése azonos magasságú, és képez egy piramis, a szög # 946;. Keresse meg a teljes felületét a piramis.
A képen egy piramis ACBO, OM-magasság, OK-apothem.
Középpontot L apothem OK, LM szöget zár be a magasságot OM # 946;.
# 916; OMK téglalap így ML a medián a háromszög, majd OL = LM = LK = m
# 916; OLM egyenlőszárú ezért ∠OML = ∠LOM, ami azt jelenti, hogy a szög formákat apothem magassága # 946; (Az ábrázolt).
Sbok = p • a / 2; ahol p - semiperimeter alapja, - apothem OK.
Az alap a piramis egy derékszögű háromszög, amelynek oldalai egyenlő. Keressük az oldalán az alap, erre használjuk a már rendelkezésre álló adatokat. Mint ismeretes, az MK az a sugara a alapkör.
r = AB * √ (3) / 6 → AB = 6R / √ (3)
Fogjuk találni, ami r, tudván, hogy a bűn # 946; = MK / OK → OK = MK / sin # 946; = 2m / sin # 946;