A medián osztja a háromszög
A medián felezi nemcsak az oldalán a háromszög. Még a medián osztja a háromszög két egyenlő részre. Lássuk, hogy ez a tulajdonság a problémák megoldásában.
Először megérteni, hogy miért a medián osztja a háromszög részekre, amelyek téren.
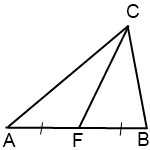
Mivel ∠AFC és ∠BFC - kapcsolódó, to∠AFC + ∠BFC = 180 °. És mivel a képlet hozza sin (180 ° - α) = sin α, a sin∠AFC = sin (180 ° -∠BFC) = sin∠BFC. Mivel az átlagos CF osztja AB oldalán két egyenlő részből áll: AF = FB, akkor van:
Mi jár, hogy fontolja meg a feladatokat, amelyekre bebizonyosodik tulajdonság alkalmazható.
Abban medián BD ABC háromszög jelöli az M pont úgy, hogy BM: MD = 3: 1. Keresse meg a ABC háromszög területe, ha a háromszög területe egyenlő AMD 3 cm.
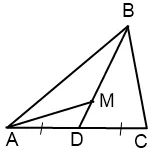
A fenti, a terület a háromszögek ABD és a CBD egyenlő. Mi kifejezetten a háromszög területe ABC révén az AMD a háromszög területe: