A nehéz kamatláb

Komplex kompaundálási kamatláb - a kamatláb, amelyen a eredményszemlélet alapján, szemben az egyszerű érdeklődés, jelentése n e r e m e n n o th. azaz kamatfizetési kötelezettség terheli kamat.

Ahogy előzetesen megállapított bizonyos egységet időszakban az érdeklődés eredményszemléletű (év, hónap, negyed, stb), és a kamat i (vagy i% = 100 i). Hagyja, hogy a kezdeti fennálló összeg van P. Ezután az egység révén egy rés összege lesz az adó S 1 = P (1+ i), mint abban az esetben egyszerű százalék. Azonban, a végén a 2. adó egység intervallum teljes S 2 = S 1 (1+ i) = P (1+ i) 2 (szemben a képletben az S 2 = P (1 + 2 i) egyszerű százalék. Végére 3. harmadban állítjuk elő az S 3 = S 2 (1+ i) = P (1+ i) 3. És így a végén az n-edik egység időszakban kapjunk

Tehát, n után időszakok a kezdeti mennyiségű p növeli (1+ i) n-szer. Módosító (1+ i) n nevezzük összetételéhez tényező. Vegye figyelembe, hogy rárakódással vegyület érdekes a növekedés kezdeti mennyiségének a törvény a mértani, amely az első ciklus, és a nevező P. 1+ i.

Probléma 1: A kezdeti betét összege P = 40,000 p. Kamatláb i% = 10% évente. Határozzuk naraschѐnnuyu a kamatos 3 évig, majd hasonlítsa össze a mennyiségét kompaundálási rendszerének egyszerű érdeklődés.

Határozat. Alkalmazása (1) képlet, van

S 3, bonyolult = P (1+ i) 3 = 40 000 (1 + 0,1) = 3 53 240 p.

Az összeg kiszámítási program keretében naraschѐnnuyu egyszerű kamat:

S 3, pr = P (1 + 3 i) = 40000 (1 + 0,3) = 52 000. <53 240 р.

Így, ebben az esetben a használata összetételéhez eredményez nagyobb mennyiségű naraschѐnnoy, hogy betétes összehasonlítva előnyös a rendszer inkrementális egyszerű százalék.

Formula összetételéhez kompaundálási (1), származtatott az egész

pozitív n. alkalmazandó nem egész t

Itt, P - a kezdeti összege, n k - k -edik időtartama kamatperiódus és i K - az egyszerű kamatláb időszakban a k.

Feladat 3. A szerződés a banki betéti szolgáltatások 4 évig fix változó sebességgel kamatos következők. Az 1. évben - 6%, a 2. és a 3. évben, ez az arány ugyanaz - 5% -os évi, a 4. év

- 8%. Határozza meg a tényező értéke, kompaundálási 4 évig.

Határozat. Legyen P - néhány kezdeti összeget. A feladat szerint

1 i = 0,06, i = 2 i 3 = 0,05, i 4 = 0,08.

Legyen i 23 = 0,05. Van képlet szerinti (2):

S = P (1, i 1) 1 (1 i 23) 2 (i 1 4) 1 = P (1 + 0,06) (1 + 0,05) 2 (1 + 0,08).

Ennek eredményeként a számítások megkapjuk az értéket összetételéhez faktor:

S / P = (1 + 0,06) (1 + 0,05) 2 (1 + 0,08) = 1,262142.

Összehasonlítás növekedési egyszerű és összetett százalék

Ugyanakkor kamatláb i accretion kompaundálási:

gyorsabb, mint az egyszerű kamat, ha az időtartam hossza az eredményszemléletű több mint egy időszakban;

Ez lassabb, mint az egyszerű érdeklődés, ha a hossza az időszak kevesebb, mint egy egyetlen kompaundálási időszakban.

Korábban azt is megjegyezte, hogy a növekmény pénzt ugyanebben az időszakban, függetlenül attól, hogy a rendszer az egyszerű vagy összetett százalék.

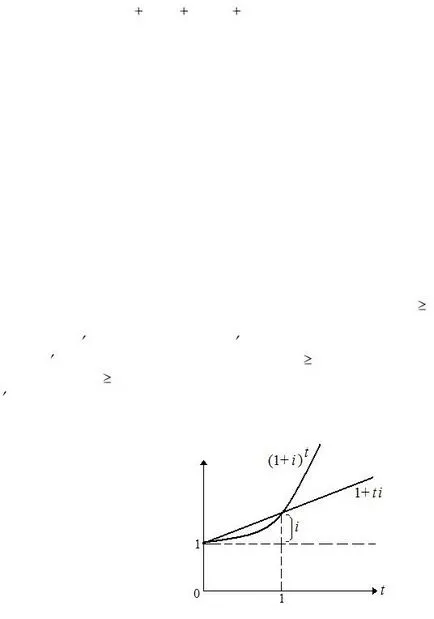
Lássuk be a fenti. Valójában, amikor a i> 0:

ha t> 1, akkor (1+ i) t> 1+ azt; ha 0

Ennek bizonyítására, Tekintsük az f (t) = (1+ i) t és g (t) = 1+ azt. Nyilvánvaló, F (0) = g (0), F (1) = g (1), és mindkét funkciót növekedni t 0 nem csak az értelmes értelemben, hanem figyelembe véve pozitivitás formálisan származékok f (t) = (1+ i) t ln (1+ i) és g (t) = i. Ugyanakkor, a másodrendű származékot f (t) = (1+ i) t 2 ln (1+ i) pozitív a t 0, ami azt jelenti, lefelé irányuló konvexitás f (t) a t 0 (azaz, felgyorsult növekedés) . A funkció g (t) nő lineárisan

A grafikon azt mutatja, az f (t) = (1+ i) t és g (t) = 1+ hogy attól függően, t:

Példa. Legyen az összege P = 800 növekszik az arány i = 8% egyszerű és összetett százalék. Aztán naraschѐnnye összegek

Annak érdekében, hogy értékelni lehessen kilátásai hitelezők és az adósok gyakran fontos tudni, hogy hány alkalommal a kölcsön összege megnövekszik N-szer egy adott kamatláb i. Hogy kiegyenlíti ez a tényező összetételéhez a N értékét, mint amelynek eredményeként kapjuk:

a) egyszerű százalékban 1 + Ni = N. ahol n = (N -1) / i.

b) elegyítési (1 + i) n = N. ahol n = ln N / ln (1 + i).

Probléma 4. Számoljuk ki az évek az adósság növekedése, amelynek mértéke kétszerese az egyszerű és kamatos kamat évi 4%. Az eredményeket összehasonlítjuk.

Határozat. A probléma feltétel i = 0,04, N = 2. van

a) az egyszerű érdeklődés n = (N -1) / i = 1 / i. ahol n = 1 / 0,04 = 25 év

b) elegyítési n = ln N / ln (1 + i), ahol n = ln 2 / ln (1,04) 17,67 év. A számítás a kamatos kamat rendszer megduplázódik az adósságot.

Bizonyos szempontból a kamatok egy törtszám évek

A gyakorlatban a pénzügyi intézmények törtszámok évek t kamatszámítás másképp. Tekintsük a három fő módja a töltés.

1. összetételéhez képlet: S = P (1+ i) t.

2. alapján a kombinált eljárással, amely szerint a egész számú éves összetételéhez érdeklődés, és egy frakcionált - egyszerű: S = P (1+ i) n (1+ bi), ahol t = n + b. n - egy egész szám s, b - a tört része egy év.

3. A számos kereskedelmi bank alkalmazott általában összhangban van az időt, amelyre a kisebb az elhatárolás időszak nem kamatozó, azaz

Probléma 5. A méret által nyújtott hitelek 27 hónap 100 000. Az éves kamatláb 20%. Számolja naraschѐnnuyu kifejezett összegek három módon.

Határozat. A feladat szerint a kölcsönzési idő 2,25 év. Jelenleg a következő számításokat.

Szerint az 1. módszer: S I = 100 000 (1 + 0,2) 2. 2 5 150 715 p. 46 kopecks. Szerint a 2. módszer: S II = 100 000 (1 + 0,2) 2 (1 + 0,25 0,2) = 151 200 p. A 3. módszer: S III = 100 000 (1 + 0,2) 2 = 144 000 p.

Formula diszkontálás, amikor az elegyítést

A matematikai képlet diszkontálás

Ha diszkontálás szerint kell elvégezni a rendszer a banki (kereskedelmi) számviteli, a kezdetben egyeztetett diszkontráta d. d 0 <1. Она применяется не к начальной сумме, как при простой учетной ставке, а к сумме, уже дисконтированной на предыдущем промежутке времени. Размер дисконта, или учета, удерживаемого финансовым учреждением, равен

Feladat 7. eszköze az összeg 20 000 p. a kifejezés kifizetése előforduló 1,5 év, elszámolni kamatos mértéke 18% évente. Határozza meg a kapott összeg a bejegyzett tulajdonosa a számlát, és a megfelelő kedvezményt.

Határozat. Itt, a feltétellel feladatok S = 20 000, n = 1,5, d = 0,18. Ezután a képlet (4) kapjuk a következő számítási eredmények:

a kapott összeg a tulajdonos P = 20.000 (1-0,18) 1.5 14850 o. 83 kopecks.

akciós D = S - P 20 000 - 5149 = p 14850,83. 17 kopecks.