A problémák megoldását a differenciálegyenletek és sorozat, 3. oldal
Váltakozó sorozat, ezért a következménye funkció Leibniz. Nyilvánvaló, hogy a harmadik kifejezés a sorozat, így n = 2 és legfeljebb 0,001:
.
Kiszámítására, például be kell állítani, hogy radiánban.
b) kiszámításához az első jelen, tehát, hogy írunk:
.
Következő lépésként alkalmazza a binomiális sor, ahol hisznek. Esetünkben :.
Mi valósult meg a számot, majd
,
.
Mivel a harmadik tag, ezért, és pontossággal 0,001 :.
4.11. Kiszámítása integrálok segítségével sorozat
Mivel a teljesítmény sorozat Terminusonként lehet integrálni minden szegmensben fekvő intervallumon belül a konvergencia, majd bővül az integrandus a hatványsor lehet találni egy közelítő értéket a határozott integrál.
Példa 1. Számítsuk megközelítette a legközelebbi 0,001 határozott integrál :.
Határozat. Az integrandus olyan, hogy a primitív nem lehet kifejezni elemi funkcióit. Alkalmazható egy számot, ezt kapjuk:
,
,
mivel a harmadik tag kapott váltakozó sorozat kevesebb, mint 0,001.
Példa 2. Számítsuk mintegy legfeljebb 0,01 integrál:
.
Határozat. Antiderivált funkció sem lehet kifejezni elemi funkciók:
,
minden x (mi itt is egy Maclaurin sorozat a funkciót)
Ahhoz, hogy értékeljék a fennmaradó eredménye Leibniz funkció nem működik, mivel a váltakozó sorozat nem kapunk. Következőképpen járjon el:
.
A zárójelben kapott összeget végtelen mértani, amely 1 :. Ezért.
Kiszámítása a jogot ez az egyenlőtlenség a különböző n (n = 1, 2, 3, 4), azt látjuk, hogy az n = 4 :. Ezért, hogy kiszámítja a szerves legfeljebb 0,01 elegendő, hogy S4. azaz
.
4.12. Hozzávetőleges oldatot differenciálegyenletek
Néha pontosan integrálni a differenciálegyenlet nem sikerül. Ebben az esetben célszerű keresni a megoldást formájában hatványsorba.
1. példa adott differenciálegyenlet. Megtalálni egy adott oldatban kielégíti a kezdeti feltétel y (1) = 1, formájában egy Taylor-sor (figyelembe az első 5 tag).
Határozat. Hagyja, hogy a megoldás
A kezdeti feltétel y (1) = 1, az első kifejezés a sorozat. Behelyettesítve x = 1 és y = 1 az egyenletben, kapjuk :.
Mi különbözteti meg az eredeti egyenletet:
, , ,
, ,
stb Mi helyettesíti az értékeket talált a sorozat, kapjuk:
6. példa 2. megtalálja az első kifejezéseket a teljesítmény sorfejtése megoldások a differenciálegyenlet, amely megfelel a kezdeti feltételek y (0) = -2.
Határozat. Mivel X0 = 0, akkor a megoldás kérik formájában Maclaurin sorozat
.
Tekintettel arra, hogy y (0) = -2. Behelyettesítve ebben az egyenletben a kezdeti feltételek kapjuk: megkülönböztetésével az eredeti egyenlet, azt látjuk, egymás után:
, , ,
, , .
Behelyettesítve az értékeket talált a sorozat, kapjuk:
.
4.13. Fourier-sor
1. példa expandált egy Fourier-f (x), amelynek egy előre meghatározott időtartam, és 2p intervallumban (-p p] a következőképpen .:
Határozat. f (x) függvény egy pont a diszkontinuitás (ábra. 4.2).
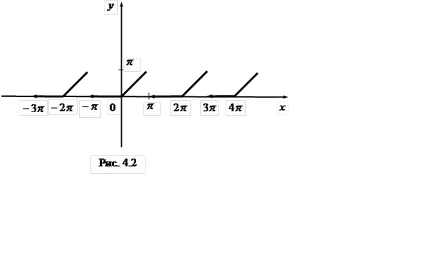
Mivel f (x) szakaszonként monoton és intervallumon [-p. p] Csak egy pont diszkontinuitás az 1. típusú (), majd az összes pontot x folytonosságának f (x) bővíthető Fourier-sor. Találunk számos tényező:
.
,
n i N. Behelyettesítve ezeket az együtthatókat egy sorban, megkapjuk:
minden, Kj Z. A pontok számát az összeget találtam:
.
2. példa bővült Fourier-sor periodikus függvény f (x) az időszakban
2L = 4, meghatározott intervallumon (-2, 2] a következő egyenlet: f (x) =.
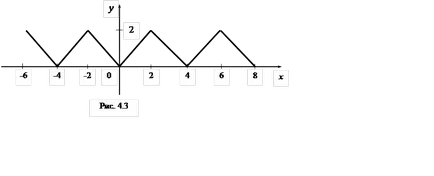
Határozat. A f (x) van definiálva, és folytonos az egész valós tengelyének és szakaszonként monoton szegmens [-2, 2] (ábra. 4.3).
Kiszámoljuk az együtthatók Fourier-sor:
,
.
Kiszámításakor milliárd használatát tulajdonsága páratlan funkció:
,
mivel az integrandus páratlan. A Fourier-sor, hogy a funkció konvergál ez a funkció minden x. Mivel f (x) folytonos minden x. Így
.
1. Közönséges differenciálegyenletek. 4
1.1. Problémák vezető közönséges differenciálegyenletek. 4
1.1.1. A probléma a szabadesés a szervezetben. 4
1.1.2. A probléma a tranziensek az áramkörben. 5
1.1.3. A probléma a radioaktív bomlás. 6
1.2. Alapvető fogalmak és koncepciók. 6
1.3. A geometriai jelentése az egyenlet. 9
1.4. A fő osztályok a elsőrendű differenciálegyenletek. 10
1.4.1. Differenciálegyenletek elkülöníthető változókat. 10
1.4.2. Homogén differenciálegyenletek. 11
1.4.3. Lineáris differenciálegyenletek. Bernoulli-egyenlet. 12
1.4.4. Közönséges differenciálegyenlet. 14
1.5. Differenciálegyenletek nagyobb megrendeléseket. 17
1.5.1. Az egyenletek, amelyek lehetővé teszik csökkentése érdekében. 17
1.5.2. Lineáris differenciálegyenlet a rend n. 21
1.5.3. Lineáris homogén másodrendű differenciálegyenletek állandó együtthatók. 24
1.5.4. Lineáris inhomogén differenciálegyenlet n-ed rendű. 28
1.6. A rendszer közönséges differenciálegyenletek. 33
1.6.1. Az eljárás megszüntetése ismeretlenek. 34
1.6.2. Rendszerek lineáris differenciálegyenletek állandó együtthatók. 36
2. Numerikus sorozat. 39
2.1. A koncepció egy numerikus sorozat. 39
2.2. Elegendő, ha a konvergencia-sorozat pozitív értelemben. 42
2.3. Váltakozó sorokban. Váltakozó sorozat. 48
3. Funkcionális sorozat. 52
3.1. A koncepció a funkcionális sorozat. 52
3.2. Hatványsorok. 54
3.3. Tulajdonságok hatványsorok. 58
3.4. Taylor sorok és Maclaurin. 59
3.5. A használat hatványsorok. 64
3.6. Fourier-sor. 67
4. A megoldás a problémára. 74
4.1. A differenciálegyenletek elsőrendű elkülöníthető változókat. 74
4.2. Homogén elsőrendű differenciálegyenlet. 74
4.3. Lineáris differenciálegyenlet az elsőrendű. 75
4.4. Differenciál egyenletek magasabb rendű, lehetővé téve csökkentése érdekében. 77
4.5. Lineáris másodrendű differenciálegyenletek állandó együtthatók. 78
4.6. Rendszerek lineáris differenciálegyenletek állandó együtthatók. 78
4.7. Jelek a konvergencia-sorozat pozitív értelemben. 78
4.8. Váltakozó sorokban. Leibniz tag. 78
4.9. Hatványsorok. Taylor sorok és Maclaurin. 78
4.10. A számítás a közelítő függvény értékét. 78
4.11. Kiszámítása integrálok segítségével sorozat. 78
4.12. Hozzávetőleges oldatot differenciálegyenletek. 78
4.13. Fourier-sor. 78
Test. 91
Szabályai végrehajtás és nyilvántartási teszt. 91
Problémák teszt. 92
Vizsgakérdések. 96