A tanulság az algebra, a 8. évfolyam a modul és a másodfokú függvény
„Nagyon sok funkció
Bárki lehet nevezni tanuló.
De csak néhány a mai
Úgy döntöttünk, hogy mondani "
A tanulmány a másodfokú függvény modul lehetővé teszi, hogy elmélyítse a diákok ismereteit az átalakulás grafikonok másodfokú függvények. A diákok nagy érdeklődéssel bármilyen feladatot modult. A fenti módszerek az ábrázolási funkciók gyakori, és használják nem csak a négyzet, hanem más funkciókat.
I. Bevezető szó a tanár
Funkció - az egyik alapvető matematikai és tudományos fogalmak, amely kifejezi a kapcsolat a változók között. Matematika mérlegeli absztrakt változókat, törvényszerűségeit kutató a kapcsolatukat, anélkül, hogy részletezném a probléma természetét. Például, egy arányban Y = X 2, vagy egy matematikus földmérő lásd függését a terület egy négyzet az oldalán, és fizikus, repülőgépek vagy hajóépítészi láthatjuk a kapcsolat Y légellenállás erő vagy sebesség a vizet a X mozgását.
Math Ugyanezen vizsgálatok ezt a függőséget az absztrakt formában, és ez határozza meg, hogy az x 2-szer Y növeli 4-szer, és ezt a következtetést lehet alkalmazni adott helyzetben.
Modul és a másodfokú függvény
Rajzoló funkciókat:- Y = AX + BX 2 + C,
- Y = AX + BX 2 + C,
- Y = Ax 2 + Bx + C
II. szóbeli munka
1) Határozza meg a száma X modul
2) Határozza meg a másodfokú, mondja minden, ami ismert erről a funkcióról (chart tulajdonságok).
3) Find a szám grafikon Y = -X + 4X 2 - 3.
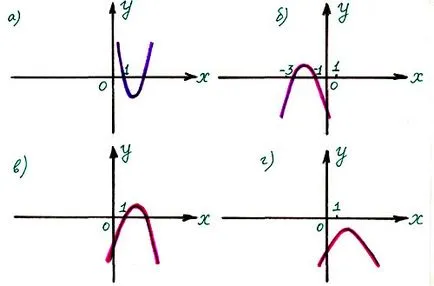
4) A mi mutatjuk a grafikon Y = - (X + 1) (2 - x)?
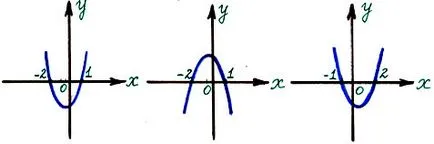
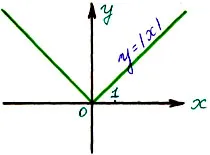
5) Emlékezzen, hogyan kell építeni a grafikon Y = X
A definíció modul
A grafikon Y = X szimmetrikus tengely Y.
III. Rajzoló funkciókat:
Elvégzett munka csoportokban, mert grafika a K-1) és a K-3) azonosak, meg kell összehasonlítani, és következtetést levonni (3 csoport). Minden csoport kiadott egy kártyát a 3 feladat. A diákok meg kell építeni grafikonok a másodfokú függvény tartalmazó modul, használatával a meghatározása a modul és megkötésére: hogyan kell építeni egy grafikont a funkció segítségével a grafikon egy másodfokú függvény és a szimmetria tekintetében a koordinátatengelyek.
Feladat. építeni egy grafikont a funkció segítségével:
a) a meghatározása a modul;
b) A grafikon a függvény Y = Ax 2 + Bx + C;
c) tekintetében a szimmetria tengely.
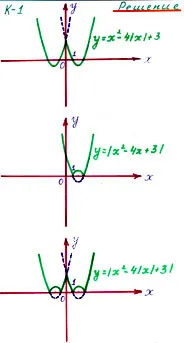
a) Y = X 2 - X 4 + 3
b) Y = X 2 - X 4 + 3
a) Y = X 2 - X 4 + 3
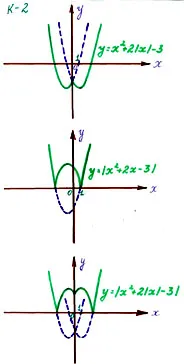
a) Y = X 2 + X 2 - 3
b) Y = X 2 + X 2 - 3
a) Y = X 2 + X 2 - 3
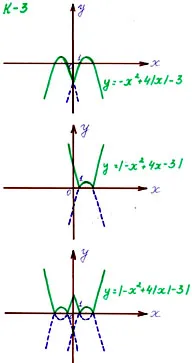
a) Y = -X + 2 X 4 - 3
b) Y = -X + 2 X 4 - 3
a) Y = -X + 2 X 4 - 3
IV. A diákok következtetni elrendezése grafikonok ezen funkciók
Kérdés: a) hogyan kell építeni egy függvény grafikonját Y = f (X)?
(1. módszer Plot függvény Y = f (X), ha X 0 és Y = f (-x) ha X <0.
2 módszer. Ábrázoljuk a függvény Y = f (X) és a jobb oldali kijelző generált szimmetrikusan Y tengely).
b) Hogyan építsünk egy függvény grafikonját Y = f (X)?
(Ábrázoljuk a függvény Y = f (X) és a pontot negatív ordináta kijelző szimmetrikusan az X tengely).
c) Hogyan építsünk egy függvény grafikonját Y = f (X)?
(Ábrázoljuk a függvény Y = f (X), ahol X jelentése 0, és ez a része a grafikon kijelző képest szimmetrikusan Y tengely, majd a negatív pont koordinátáit kijelző képest szimmetrikusan X tengelyre)
d) Miért van a grafikus funkciók Y = -x 2 + 4X - 3 és Y = X 2 - 4x + 3 azonos?
(Mivel A = A -A = A)
Úgy véljük, a függvény független változója a modul jelet. Most tekintsük a funkció, ahol van olyan funkció is, vagy a funkció, és a független változó egy időben, azaz a modulus jel típusától függően
Y = AX + BX 2 + C és Y = AX + BX 2 + C
Konkrét példákat.
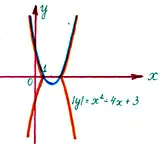
Ábrázoljuk Y = f (X) függvény, és figyelembe azt a részét, amely felett található az X tengelyen X 2 - 4x + 3 0, és adjunk hozzá a viszonylag szimmetrikus leképezés X tengely
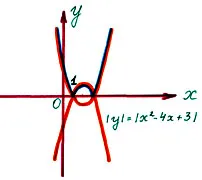
Először, konstrukció a grafikon Y = X 2 - 4x + 3. majd a pontok halmaza, amelynek koordinátái kielégítik azt a feltételt Y = X 2 - 4x + 3. azaz A grafikon Y = X 2 - 4x + 3 mutatja a relatív X tengely
VI. alkotó tevékenység
Mivel a funkció Y = X 2 + 2X- 3
Fuss az összes lehetséges átalakítások a másodfokú függvény a modullal.