A törvény a fénytörés

A fény sebessége vákuumban, körülbelül egyenlő 3 x 10 8 m / s, egy alapvető fizikai állandó. A fény sebessége minden olyan anyag mindig kisebb, mint a fénysebesség vákuumban.

Light - egy elektromágneses hullám egy hullámhossz közötti tartományban 380 és 760 nm-en, az emberi szem. KATEGÓRIA fizika foglalkozik a tulajdonságait a fény és kölcsönhatása nevű anyag optika.

Ez az első alkalom mért fénysebesség a dán csillagász O. Roemer 1676. Regisztráció az időpontokat, amikor a Jupiter holdján Io derül ki az árnyék a Jupiter, Roemer és elődei észrevették eltérések időközönként. Amikor a távolság a Föld Jupiter pillanatok Io kimenete az árnyék Jupiter késleltetett, összehasonlítva a megjósolt és maximális késleltetési 1320, amely szükséges volt a fény terjedési át a Föld körüli pályára (18A.). A nap Roemer átmérőjű Föld pályájának ítélték meg, hogy mintegy 292 millió kilométer. Elosztjuk távolság 1320 másodperc Roemer volt, hogy a fény sebessége 222.000 km / s. Ma már tudjuk, hogy a maximális késleltetés napfogyatkozás Io egyenlő 996, és az átmérője a Föld pályája 300 millió km. Ha teszik ezeket a módosításokat is, kiderül, hogy a fény sebessége 300 000 km / s.

A fény sebessége a laboratóriumban (nem csillagászati) először mérjük a francia fizikus A.I.L. Fizeau 1849 segítségével a beállítási ábrán látható. 18b. Ebben a berendezésben, a fény a forrástól 1 esemény a féligáteresztő tükör 2, és visszaverődő felé más tükrök 3 a parttól 8.66 km. A nyaláb visszaverődik a 3 tükör ismét beeső féligáteresztő tükör 2 áthalad rajta, és belép a megfigyelő szeme, 5. között a tükrök a 2. és 3. elhelyezett hajtómű 4. elforgatható egy előre meghatározott sebességgel. Ezen a fogas elfordulás törött fénysugár rövid permetezésre a sorrendben - fényimpulzusok.

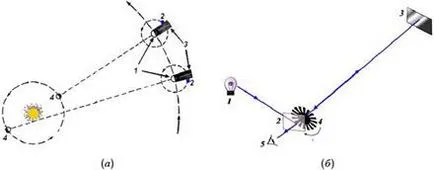
Ábra - 18 (a) - sematikus Jupiter kép (1) és Io (2) be és ki az árnyékban (3) és a föld (4) forgása során a Nap körül; (B) - beállítás Fizeau mérni a fény sebességét (fényforrás 1. 2. 3. féligáteresztő tükör Mirror 4. fogaskerék 5. megfigyelő szeme).

A beesési szög a fénysugár egyenlő a visszaverődési szög, és a beeső és visszavert sugarak határozzák síkra, amelyben szintén fekszik merőleges a visszaverő felületre, rekonstituált a beesési pontjától.

Megmagyarázni a mechanizmus a fény terjedési, a gondolkodás és a fénytörés a holland fizikus Christiaan Huygens 1678-ban javasolta a következő módszerrel (elv) építésére szaporító hullámot (Huygens-elv). Szerint a Huygens elv egy adott időpontban az egyes szaporítóanyag hullám lesz forrása a másodlagos gömb alakú hullámok. Ezek a másodlagos hullámok kölcsönhatásban áll egymással alkotnak egy hullám a következő időben.

Használja Huygens elv építésére fény hullám visszaverődik a sík felület között két médium, például a levegő és a tükrök. Hagyja, hogy a beeső fény hullám a tükör sík. azaz equiphase felülete (felületi hullám) alkotó a hullám síkjában. Ábra. 19a ábra két párhuzamos sugarak (A0A és v0v) síkban fényhullám és hullám felülete AL. A0A megfelelő beesési pontjától a tükröző felület Z0Z. A szög a tengelyei közötti ezeknek gerendák, és a szokásos, hogy a fényvisszaverő felület AY nevezett a beesési szög.

Ahhoz, hogy megtalálja a hullám felülete a visszavert hullám, meg kell határozni a borítékot a másodlagos hullámok felmerülő helyeken beesési sugarak a fényvisszaverő felület. Ha AL - merőleges v0v. Ezután, ábrán látható. 19a. másodlagos hullám pontnál következik be korábban, mint a B pontnál időintervallumban

ahol c - a fény sebessége. Ezért, amikor a gerenda v0v. Z0Z elérje a felszínt. B pontban fog okozni annak másodlagos hullám, szekunder hullám középpontja az A pontban eléri K pontot és annak sugara egyenlő lesz Miután egy ilyen konstrukció a két közbenső gerendával fényhullám, között található A0A és v0v. könnyen építeni egy félkört megfelelő hullám felületéhez a másodlagos hullámok azonos időpontban (lásd. a szaggatott vonalak és félköröket ábrán. 19a). Szerint a Huygens elv KB érintő a hullám felületei ezeket a másodlagos hullámok a hullám felszínén a visszavert fény hullám.

A bezárt szög a visszavert nyaláb b AA1 és merőleges a visszaverő felület AY úgynevezett visszaverődési szöge. Egyenletből ALB és BKA háromszögekből, hogy (1) a szög a mérlegelés megegyezik a beesési szög. Ezen felül, a konstrukció látható. 19a azt mutatják, hogy (2) a beeső és visszavert sugarak, valamint merőleges a csökkentett előfordulási pont, egy síkban fekszik. Állítások (1) és (2) az úgynevezett törvénye fény visszaverése.

Keresi a tükörben, a fényforrás látható lehet a kép (vagy a megvilágított tárgy), és a kép megjelenik ugyanaz, mint az eredeti tárgy helyezkedik el, hanem a tükör mögött, a parttól egyenlő a távolság a tárgy a tükör. Ez azért van, mert az egyes sugarak a fényforrástól felszínéről visszaverődő a O Z0Z tükröt a törvény szerint a fény visszaverése (ábra. 19b). Ennek eredményeként, visszaverődést követően a tükör gerendák alkotnak divergens, és azok kiterjesztéséből (lásd. A pontozott vonalak) metszik egymást a D pont „található, a másik oldalon a tükör azonos távolságra, mint a tárgy. Ezért a néző elé, amelyek nem tartoznak a fénysugarakat a tükör, úgy tűnik, hogy megy, és a fényforrás található, a másik oldalán a tükör. Az a pont, amely metszi a folytatása a visszavert sugarak nevezzük tükörképe a fényforrást.

19. ábra (a) - származtatása a törvény reflexió segítségével Huygens' elvet; (B) - az építőiparban a tükörképe O „a fényforrást.

Az arány a szinusz a beesési szög a szinusz a refraktív szög állandó, és egyenlő a relatív törésmutatója közötti két médium.

Amikor a fény eléri a felület két átlátszó média, része visszaverődik, és a maradék áthalad a határt. A fénytörés a változás irányát a fény terjedési ahogy áthalad a határ két médiában.

Fénytörés annak a ténynek köszönhető, hogy a különböző környezetekben a fény különböző sebességgel. Mi meg, hogyan az irányt a fény terjedési segítségével Huygens elv. Tegyük fel, hogy Z0Z sík felületen két adathordozó (1 és 2) esik lapos fényhullám, amely két párhuzamos gerendák és A0A v0v. és hullám felülete megegyezik a AL A0A sugár esik ezen a határon.

Ahhoz, hogy megtalálja a hullám felülete fényhullám továbbított közeg 1 közepes 2 (a megtört hullám), boríték határozza szekunder hullámok a 2. közeggel felmerülő helyeken beesési a felszínre Z0Z. Mivel AL - merőleges v0v. A másodlagos hullám pontnál következik be korábban, mint a B pontnál időintervallumban

ahol c1 - fénysebesség a közeg 1. Ezért, amikor a nyaláb v0v. Z0Z elérje a felszínt. 2. tápközegben okoz a másodlagos hullám, szekunder hullám középpontja az A pontban eléri K pontot és annak sugara egyenlővé válik

ahol c2 - a fény sebessége olyan közegben 2. Ezek után a két konstrukciót a közbenső fényhullám sugarak, és a között helyezkedik A0A v0v. könnyen építeni egy félkört megfelelő hullám felületéhez a másodlagos hullámok egyidejűleg. Szerint a Huygens elv KB érintő a hullám felületei ezeket a másodlagos hullámok a hullám felületre kerül megtört fény hullámai.

B közötti szög a megtört fénysugár és a normális, hogy AA1 Z0Z. úgynevezett törésszögét. majd

ahol n - állandó, az úgynevezett relatív törésmutatója. Így, az arány a szinusz a beesési szög a sine a szög fénytörés egyenlő az állandó értéket a két közeg - a relatív törésmutatójú. A készülő szerkezetek látható. 20b azt mutatja, hogy a beeső és a megtört sugarak, valamint merőleges a csökkentett előfordulási pont, egy síkban fekszik. Az előző két állítás együtt alkotják a törvény fénytörés.

A relatív törésmutató arány egyenlő a fény sebessége a közegben 1 értéke a közepes 2 (ld. 118.). Ha a közeg 1 vákuum, a törésmutató, amelynek kiszámítása a következő képlettel (118), az úgynevezett abszolút törésmutatója a közeg 2, N2. ami nyilvánvalóan mindig nagyobb, mint 1 következik (118), hogy a kifejezés érvényes bármely két média:

ahol n 1 és n2 - abszolút törésmutatójuk az 1. és 2. A közeg a kisebb abszolút törésmutatója úgynevezett kevésbé optikailag sűrű.

Szerint (118, 119), amikor a nyaláb esik egy kevésbé sűrű optikai adathordozón egy sűrűbb, például a levegő-víz, a törési szöge mindig kisebb, mint a beesési szög. Ezzel szemben, ha a fény mozog egy optikailag sűrű a kevésbé sűrű közegben, a szög fénytörés mindig nagyobb, mint a beesési szög. Mivel azonban a törésszögét nem haladhatja meg a p / 2, ami azt jelenti, ha b # 972; lshih megtört fénysugár beépítési szög hiányozni fog. Ezt a jelenséget nevezzük teljes belső visszaverődés, mint könnyen látható, hogy akkor történik, amikor