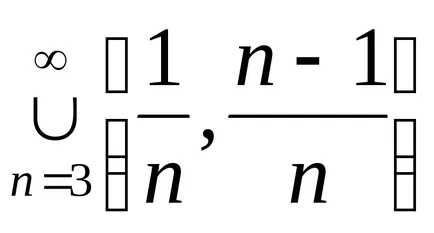áramkör készlet

Definíció 3. Legyen X - metrikus tér, M  X és H. A lényeg a neve a határ tochkoyM. Ha bármely ponton van egy szomszédságában M \ a>. Ez azt jelenti, hogy bármilyen környékén vannak pontok M eltér.

Notes. 1. A határpont, hogy hogyan tartozik, és nem tartozik a készülékhez. Például, a 0 és 1 sokasága van határpontok (0,2), de ez nem az első tag és a második tag.

Ponthalmaz M nem lehet a határpont. Ebben az esetben az úgynevezett izolált pont M. Például, 1  izolált pont (1,0) .

Ha a határpont, és nem tartozik a beállított M van egy sorozata pontok xn M. konvergáló és ebben metrikus tér. Ez elegendő ahhoz, hogy a nyitott labdákat a ponton a sugár 1 / n, és választani minden golyóstollal tartozó M. Ezzel szemben, ha van ilyen szekvencia, a lényeg az a határ.

DEFINÍCIÓ 4. A lezárás M az unió M a beállított határérték pont. kijelölés

.

Megjegyezzük, hogy a labda bezárása nem feltétlenül esik egybe a zárt labdát az azonos sugarú. Például, egy diszkrét térben a labdát áramkör B (a, 1) egyenlő a labda (áll egy a) pontban, míg a zárt labdát

(A, 1) az egész teret.

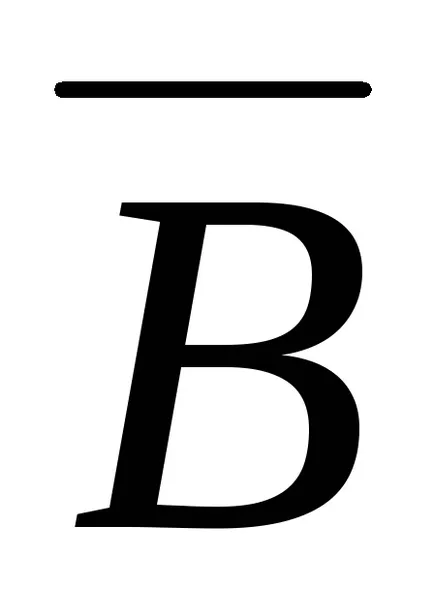
Ejtünk néhány tulajdonságait áramkör készletek.

M 

. Ez közvetlenül következik a meghatározása a lezárás.

Ha M jelentése  N.

. Valóban, eslia ,Egy M. majd minden környéken van egy pont a M. Ezek a pontok N. Ezért . Mert pont módos egyértelmű a meghatározás.

.

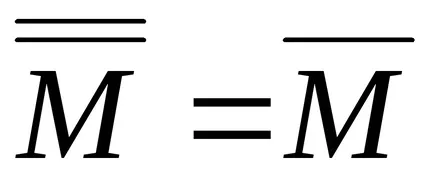
A lezárás az üres halmaz üres. Ez a megállapodás nem következik az általános meghatározás, de ez természetes.

MEGHATÁROZÁSA 5. A beállított M  X úgynevezett zárt. ha

= M.

Egy több MX úgynevezett sűrű X, ha

= X.

DEFINÍCIÓ 6. A pont a belső pontját a beállított M, ha B (a, R) M néhány pozitív r, t. E. belső pontját tartalmazza a készlet egy bizonyos környéken. A pont a külső pont a beállított M. Ha a labda a B (a, r) ​​H / M néhány pozitív r. t. e. a belső pont nem szerepel a készlet egy bizonyos környéken. Pontok, amelyek sem a belső, sem a külső pontok M. nevű határ.

Így a határpont az jellemzi, hogy minden egyes pont a közelben van belül és kívül egyaránt az M.

Állítás 4. Annak beállításához nyitva akkor és csak akkor, ha az egész pont volt a belső.

Példák zárt halmazok vannak egyenes [a, b], [a, ). Open - (a, b), (a, ). A készlet [a, b) nem nyitott és nem zárt (nem tartalmaz határpont b. A komplementer halmaz nem tartalmaz határpont a). Minden X metrikus téren és az üres halmaz  A megállapodás 5. egyaránt nyitott és zárt. A diszkrét metrikus tér egy részhalmaza mind nyitott és zárt.

Az ingatlan 3 következőképpen áramkörök, hogy ötvözi a két (és így bármely véges család) zárt zárt halmazok. Ugyanakkor, az unió végtelen családját zárt halmazok nem lehet bezárni, például

= (0, 1).