Egyenértékű elemi transzformációs mátrix, és

Elemi átalakulás a sorok a mátrixok nevezzük sorok következő átalakításokat:

1. sor szorzás egy nem nulla egész szám;

2. Az átrendeződés a két vonal;

3. A felül az egyik sor a másik vonalak, szorozva egy nem nulla szám.

Ha a mátrix egy mátrixot keresztezzük felhasználva ekvivalens transzformáció a sorok, a mátrixok egyenértékűek, és képviseli.

Példák elemi transzformációk,

Mutassa az összes elemi mátrixok átalakítani a példa

Szorozzuk az első sorban a mátrix két, azaz minden egyes eleme az első sor kell szorozni a két, akkor olyan eredményt kapjunk mátrixot. egyenértékű egy adott mátrix:

Változás az első és második sora a mátrix megkapjuk egyenértékű mátrix:

Az első sorban a mátrix vonjuk ki a második sorban, megkapjuk az egyenértékű mátrix:

Ennek eredményeként arra a következtetésre jutunk, hogy a mátrix és az ennek megfelelő, egyikük odament a másik révén egyenértékű átalakulások a sorokat.

Kronecker - Capelli

A lineáris egyenletrendszer konzisztens, ha, és csak akkor, ha a rangot a fő mátrix megegyezik a rangot annak kiegészített mátrix, a rendszernek van egy egyedülálló megoldás, ha a rang megegyezik az ismeretlenek száma, és egy végtelen számú megoldást, ha a rang kisebb, mint az ismeretlenek száma.

Komplex számok. Összeadás és szorzás

Komplex [1] a (elavult képzeletbeli száma [2].) - a fajok száma. ahol - a valós szám - az imaginárius egység (az az érték, amelynek egyenlőség :). A készlet minden komplex számok számtani műveleteket egy mező, és általában jelöli a latin. komplex - szorosan összekapcsolódnak.

Ez azt jelenti, hogy a (két komplex szám egyenlő akkor, ha azok a valós és a képzetes rész).

25) Ha. majd a számot nevezzük komplex konjugált számának.

Azaz, a konjugált komplex számok a valós részek azonos és különböző képzeletbeli jel.

Például. A komplex konjugáltját az a szám.

A komplex síkon komplex konjugált kapott számok tükörképei egymásnak tekintetében a valós tengelyen.

Tulajdonságai komplex konjugált számok

1) Ha. arra lehet következtetni, hogy a szám érvényesnek tekinteni.

2) Minden komplex szám összege - az aktuális szám.

Például. Let. akkor. majd

3) Egy tetszőleges komplex szám terméket.

Például. Let. komplex konjugált számok. majd a terméket

4) A modulok komplex konjugált szám egyenlő. és az érvek különböző jel (1.).

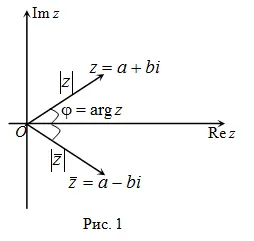
9) Ha - komplex konjugált számok, akkor