egyenlő oldalú ötszög
Szabályos ötszög gyakran megtalálható a szerkezet egy kettős pár dodekaéder és ikozaéder. Az építőiparban a sokszög, különösen a „kézzel” - segítségével egy vonalzót és iránytű, gyakran észrevehető hiba nagysága a oldalon. Például, ha osztva kerületileg öt egyenlő részre geometriai módszerrel vagy egy együttható (l = dk), az akkord nem mindig következetes méretű.
Minden létrehozására alkalmas szabályos ötszög on - egyedülálló. A legegyszerűbb módja annak, hogy építsenek n-terek, ha egy számítógép, például egy szoftver alkalmazás Corel Draw. Csak akkor nyissa meg a menüt objektumra, jelölje ki a sokszög eszköz (ötszög), kattintson és húzza a kurzort a kívánt helyre - a rajzablakban meghatározásával a kívánt méretű darabokra. Lenyomva tartja a Ctrl billentyűt, egy képet egy egyenlő oldalú sokszög. Ahhoz, hogy adja meg az oldalak számát, illetve a sokszög csúcsai a kiválasztási, majd adagoljuk a megfelelő központ értéket a csúcsok száma, vagy oldalán egy sokszög.
Amikor létrehoz végigsöpör háromdimenziós prototípus, nem zárja ki különböző módokon n szögű formák, beleértve az út „kézzel”. Egy egyenlő oldalú ötszög módszert alkalmazza dinamikus téglalap.
Szabályos ötszög természetesen lebomló saját átlója, amelynek építése adnak pentagram - ötszögű csillag. A központ egy ötszög. A top - pont a pentagram oldalon. Minden pont elosztja a megfelelő oldalán egy öt-ágú csillag a két arányos részével. Ismeretes, hogy az arány a hosszabb szegmens kevesebb körülbelül 1 618: 1, amely közvetlenül kapcsolódik a „aranymetszés”.
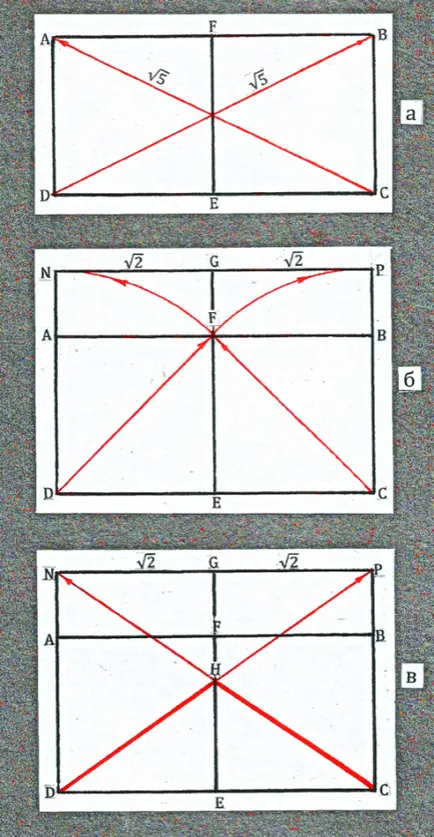
Ábra 37a ábra egy ABCD téglalap. Két négyzetek. Átlók egyenlő - átfogó egy derékszögű háromszög.
37. ábra B ábrán egy séma felépítésének két átlója a téglalapok alapján CF és DF megfelelő négyzetek. Kaptunk arányos NPCD téglalap.
A metszéspontja az átlók adnak H - felső ötszög építés alatt, valamint annak két oldalán HC, HD és CD átlós (37. ábra a.).
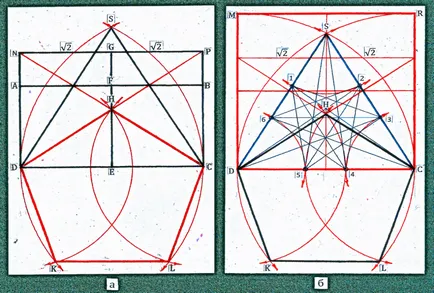
Ábra 38a ábrán egy séma látható megépítésének többi oldala a ötszög át a kereszteződés további ívek C és D pont, mint a központok a körök.
Az átlós CD (ábra. 38b), a két ív beállított pontot a 4. és 5. osztoznak az átlós ötszög megfelelően az „arany” arányokat. Ez a diagram van osztva három alak, amelyek közvetlenül kapcsolódnak a dodekaéder - dodekaéder. Ábra HCLKD - annak ötszögű arc, MRCD számadatok és SCD - n -gons korlátozása kis átlós síkjában részén egy dodekaéder. Az SCD oldalú háromszög síkja tükrözi Folytatása kettős ikozaéder.
A javasolt rendszer lépésről lépésre építése egy szabályos ötszög vezet minket, hogy a borda-háló modell egy kettős pár - ikozaéder és a dodekaéder. Reakcióvázlat (Függelék, ábra. 80) tartalmaz a monochertozh. Ez a kép a sokszögű alakzatok, amelyek korlátozzák az átlós síkja vonalszakasz mesh-modell egy kettős pár szabályos poliéderek.
Megértése elvének kiterjesztése síkok Az arcok és a rajz módszer (diagramok), garantálja a sikeres mastering technikák morfogenezisben, például csillag poliéderek. Minden helyes (isohedral) és semiregular (nem isohedral) rendre egyenlő poliéderek képező bordák. Ellentétben a platóni, arcok felhajtóerő szervek nem egyenlő egymással. Arcuk egyenlő szárú n-terek, különböznek méret (1. ábra, 10. ábra -. 23).
Köztudott, hogy minden platóni és archimédeszi poliéder lehet helyezni a gömböt. A központok metszéspontjában keletkező a szimmetriatengelye egybeesik a a gömb középpontja. Ez a tény azért fontos figyelembe venni, amikor méretének meghatározásakor csillag poliéderek. Fontos az is, hogy a mérete az első és az azt követő nyert formában kiterjesztések változik az irányt a növekedés. A módszertani szempontból, mint egy szemléltető anyag hasznos, hogy egy „lánc” elrendezések szekvenciálisan, egymást követő térbeli formákat.
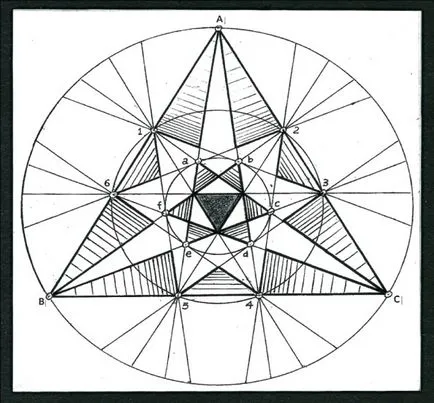
A 39. ábra monochertozh ikozaéder. Rajta vannak jelölve csúcsok a, b, c, d, e, f, amely egybeesik a kis kör. Rajtuk keresztül a háromdimenziós tér kétszeres szimmetriatengely.
Síkidomok, kikelt belső kerülete alkotnak egy háromdimenziós térben tetraéderes szögek. Ezek egyesül stellate formában - a vegyület öt octahedra, ábra. 40 (4).
Következő átlagos kör metszi a pont 1-6. Ezek a pontok a csúcsai poliéderek stellate ismert: a harmadik, hetedik és kilencedik formája az ikozaéder (4). A 41. ábra stellate alakja úgynevezett „tíz tetraéderek vegyület”.


A központban a rajz (. 39. ábra) van egy egyenlő oldalú háromszögben - egyike a húsz arcok az ikozaéder. Ahhoz, hogy az oldalán szomszédos egyenlő szárú háromszögek, melyek kombinálva vannak háromszögletű szögek háromdimenziós térben. Ezek a sarkok alkotják a háromszög alakú piramis. Base a piramis egybeesnek az arcok a poliéder, és képezi az első csillag alakja ikozaéder, ábra. 42 (4).


Külső nagy kör (ábra. 39) keresztezi az A pont, B, C. Ez a csúcs több csillag formációk együtt fut szembe fogságban csillag alakú. Sík elemek képező konvex - homorú szerkezet tízlapú szög kikelt kerülete körül egyenlő oldalú háromszög ABC. Tizenkét ilyen struktúrákat lehet elhelyezni, mint a „kivitelező”, az arcán egy dodekaéder, és el ragasztószalaggal. Ennek eredményeként ez a hézag képződik stellate formában nagy ikozaéder (4). Ez a forma nevéhez Kepler-Poinsot (ábra. 43).
A kivonat a monochertezha szükséges alkatrészek háromdimenziós alakzatok lehet pre-sorszámozva modell poliéder élei, és jelölni azokat a diagram (grafikon) csoportok szimmetrikus síkok (ábra. 44).
Együttesen ezek a vizuális modellek lehetővé teszik, hogy milyen mértékben, hogy ellenőrizzék a sorrendben kiterjesztett síkok a felületek sík területen, és egy rajzot az űrben. Ebben az eljárásban az a borda-háló modellt jelentősen tovább behatolását a háromdimenziós szerkezet, hogy továbbra is.
A folyamat során a kicsomagolási szükségtelen számításokat végzi a paramétereket a sík tag (n-szén rekeszek) a monochertezha. Ő kétdimenziós vetülete tartalmaz természetes metrikus információk sík geometriai formák. Nyomok többirányú kiterjesztett síkok a poliéder metszik a rajz síkjában. Ravnogrannik néha a sejtmagban.
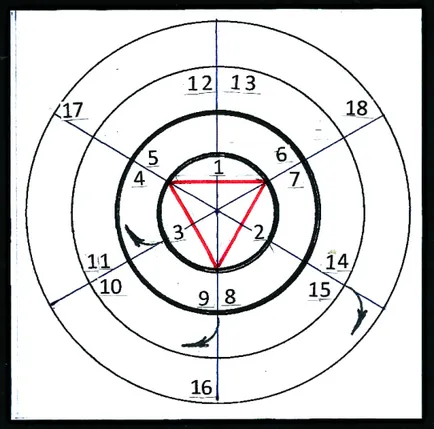
Tekintsük szimmetrikus ikozaéder csoport repülőgépek. A grafikonon (ábra. 44) arcok számokat. A központban a gráf egy szabályos háromszög - feltételes szélén
ikozaéder. Átmérősen szemben a vonal párhuzamos azt nem mutatja az ábra. Két kör középpontja körül a háromszög mutatja tömör, vastag vonalak. Ezek számának korlátozására látható arcok a modell a ikozaéder, nézve a felső oldalon arcát. A harmadik és a negyedik kerületi számának korlátozása láthatatlan arcok. Ők képviselik a vékony vonalak. a szimmetriatengely áthaladnak a csúcsok és felezőpontja az oldalán a háromszög. A számok kapcsolatos egy bizonyos kör, meghatározza az arcok száma (felületek), tagjai a megfelelő szimmetrikus csoport.
Az első csoport - a számok 1.2.3; A második csoport - 4,5,6,7. 8. 9; A harmadik csoport - 10.11.12.13.14.15; negyedik csoportot - 16.17.18. A nyilak jelzik az átmenet az egyik kört a másikra.
A repülőgépek száma szimmetrikus csoport korrelál a sávok számát a kétdimenziós mező monochertezha. Síkokat az első csoport szimmetrikusak szegmensek 1.4; 2,5; 3.6. Nyomokban második sík szimmetrikus csoportok - szegmensek 1.3; 3,5; 1,5; 2.6; 2.4; 4.6. Nyomokban harmadik síkba szimmetrikus csoportok - szegmensek A4; A5; B2; B3; C1; C6. Nyomai negyedik síkok szimmetrikus csoportok - szegmensek AC; BC; AB (39. ábra).
A folyamat folytatódott arcok a poliéder vezet, hogy a különböző térbeli formák. Ez a téma már jelentős figyelmet kapott a kutatók (4, p.228, 229). Elérhetővé vált az eredmények matematikai felfedezés terén sokoldalú osztályozási szervek. Ez különleges helyet foglal csillag poliéder.
Létrehozása elrendezések stellate struktúrák, a diákok gyakran szembesülnek kielégítő eredményeket ad pontos építési monochertezha. A rajz egy leképezés a síkot, amelyen az összes többi felületet a sík kiterjesztett maradnak nyomok.
Összpontosítva metsző síkok poliéderes szervek, lehetséges hangsúlyozni, hogy az általunk javasolt borda mesh modellek tükrözik az elv vágási helyet.
A grafikon (ábra. 44), és a leírás vezethető eloszlása tizennyolc pályák kiterjesztett síkok (ábra. 45).
Tekintsük a geometriai rend építési monochertezha gyakran ábrázolják az oldalakon ez az anyag. 45. ábra monochertozh korlátozott kiterjesztését sík néz nyomai a nagy ABC háromszög. Emlékezzünk, hogy annak három oldalát - nyomait egyik a négy szimmetrikus csoportok síkok néz az ikozaéder. Az építkezés csökken egy egyszerű grafikus műveleteket. Körsugár szabaddá, majd elosztjuk hat részre. Feltéve, egyenlő oldalú háromszög ABC három pontot elosztjuk a kerületet. A BC oldalon épített két merőleges - BD és CE, amelyek áthaladnak a szabad kerülete a szétválás pont. Keresztül háromszöget tartott vízszintes egyenest. Zárt oldalán alkotó téglalap BDEC, ami bele van írva az ABC háromszögben. A téglalap van osztva rács, amely tizenkét sejtek. Az eljárás az a rács könnyen meghatározható a benyújtott rajz.
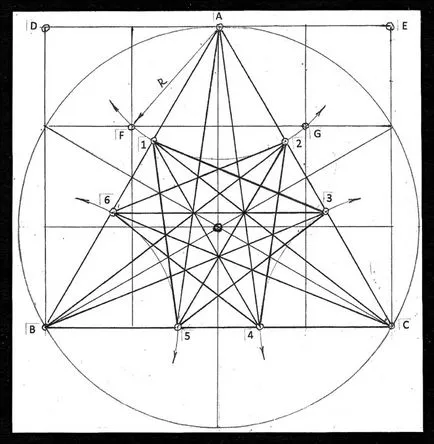
Miután a nagy háromszög közepén végzett három bisectors hogy csatlakoztassa a csúcsokat A, B, C ingyenes kerületi elválasztó pontokat.
Ebben a szakaszban az összes pontot a geometriai építési végrehajtásához szükséges vízszintes és függőleges rácsvonalak, amelyek a rajzban. Három oldalról (nyomok) ABC háromszög keresztezik tizenöt pályák fennmaradó három csoport szimmetrikus sík. Ehhez mindkét oldalán a háromszög van állítva két pontot, amelyek mindegyike osztja az oldalsó kapcsolatban a „aranymetszés”. Például, az arány a AB vonal (ábra. 45), hogy a szegmens A6 „arany” arányokat.
Pontoktól A, B, C, mint a központ, AF vagy AG nagy sugara a háromszög oldalainak metszik a kívánt ponton 1,6; 2.3; 3,4; 4.5. Set pont az oldalán a nagy háromszög vannak összekötve egyenes szakaszokkal. A formáció két egyenlő oldalú háromszög kapott összefüggés páratlan (1. 3. 5), majd a páros (2. 4. 6) pont. Három egyenes vonalak vannak kötve páronként vertex A, B, C fekvő pontok lehetnek ellentétes oldalán a háromszög. A rajzon egyenes vonalat kell húzni az oldalakkal párhuzamosan AB, AC, BC, keresztül pontpárt 1,4; 2,5 és 3,6. Ennek eredményeként, egyszerű geometriai konstrukciók, rajz kapunk, amely az úgynevezett „sablon” (4) vagy a „monochertezh” (2).
A 46. ábra egy rajz a végső folytatása a ikozaéder. Nyomai annak folytatására külső felületén a kör, nem kereszt, nem számít, mennyire nem folytatódott. Vége vágási síkjait térben rekeszek monochertezhe árnyalt. Úgy tartják, hogy egy lefutó csillag alakú ikozaéder (4, 110. oldal).

A kép nem kijelölése az előző 45. ábra rajz „tiszta” formában sík elemek kialakítása lehetővé teszi, hogy érzékelik a különálló rekeszek. Ez különösen fontos a replikáció az n-gon monochertezha. Módszer perekalyvaniya azok tűt a munkadarab elrendezés lehetővé teszi, hogy megkapjuk lapos elemek dörzsárak.
A konstrukció a végső rajza a folytatása az ikozaéder, elég ahhoz, hogy meghosszabbítja a vonalak (nyomokban) kívül az ABC háromszög, hogy a kereszteződés (ábra. 45). Vegye figyelembe, hogy néhány, a sorok el fog térni, és néhány keresztezik egymást. Túl a metszéspontja a tizennyolc vonalak (sávok) el fog térni a párhuzamos pár. A hosszabbítás a rajz (ábra 0,45) nem garantálja a megszüntetése hiba síkidomok épített elrendezést.
Tekintsük 46. ábra a kivitelezést, mint korábban, a Division kerülete hat részre, valamint az egyszerű geometriai építési technikákat. Egy iránytű oldatot egyenlő a kör sugarát, ez a módszer a választóvonal végezzük.
Ahhoz, hogy osztja a kör egyenlő részekre, tetszőleges számú egyszerű képletet használjuk: l = dk. ahol l - húr hossza, d - átmérője az előre meghatározott kerülete és a K - faktor. Például, osztani egy kör öt egyenlő részre az együttható értéke 0, 58779, és a hat - 0,50000 stb
Ábra 46 felső véglap tagjai, megszüntetéséről folytatása tartoznak külső kerülete. Ahogy az előző ábrán 45 osztály pontot épített egy nagy szabályos háromszög. Közepén keresztül a kör és a háromszög csúcsai felezik. Metszik egymást a felek és a kör. A kapott pont az oldalán a nagyobb háromszög párokat köti össze egyenes vonalak hosszabbítani addig, amíg metszi a külső kerületén. Keresztül a tetején a kis szabályos háromszög halad a belső kör. Az oldalon kis háromszög vannak elrendezve két pont alapján egy téglalap alakú rács olyan módon, hogy már leírták (ábra. 45). Ezeket a pontokat lehet beállítani másképp. Mert ezen a ponton kapcsolódik minden csúcsa a nagy háromszög egymással szemközti pont egy nagy kör, amely lehetővé teszi a bővítmények oldalon kis háromszög. Így kialakított vonalak keresztezik kis háromszög oldalainak és így a kívánt osztási pont.
További építési nyomai kiterjesztett síkok végezzük a leírások a 45. ábrán.
Most leírjuk egy másik módszer lehet kiválasztani a választóvonal pont egy ikozaéder háromszög oldalai rajz. A kép (ábra. 47) tartalmazza a rajzon, a szétválás pontokat, amelyeket úgy kapunk egy téglalap alakú háromszög. Először, össze egy derékszögű háromszög a kapcsolat 1: 2, és egyenlő oldalú háromszög ABC.

Másodszor, az ív hajtjuk a D pont, mint a központ DB a kör méretét, hogy a kereszteződés a átfogója DC. Harmadszor, hogy egy második ív C pontból CE méretét, hogy a kereszteződés a háromszög alapja. F pont - pont elosztjuk az oldalán egy egyenlő oldalú háromszög. BF szegmens minden csúcsa az ABC háromszög vannak beállítva az oldalán pontpárt: 1,6; 2.3; és 4.5. Három oldalról (AB, AC, CB) nyomai egyik szimmetrikus csoportok terjeszteni arcok az ikozaéder. Tizenöt nyomokban maradt monochertezhe folytatásai megfelelően osztják el a leírás, hogy a 45. és 46. ábrán.