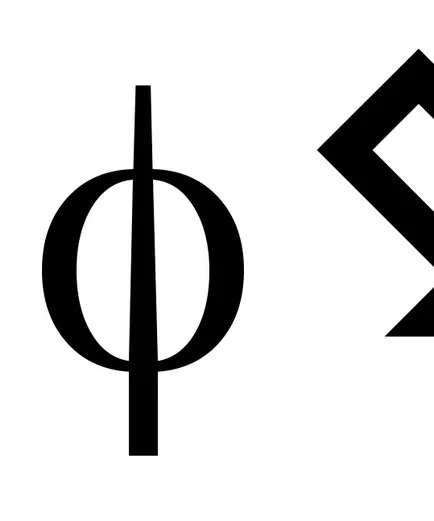
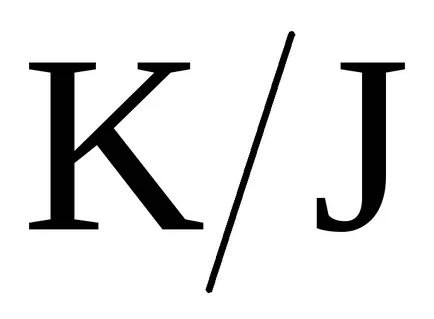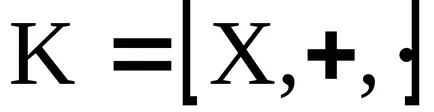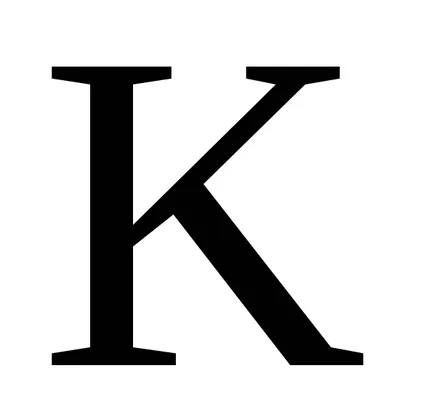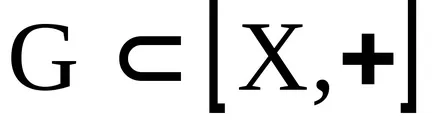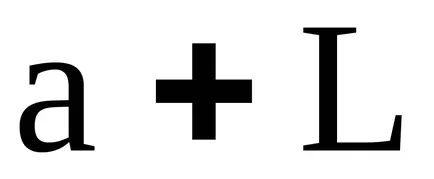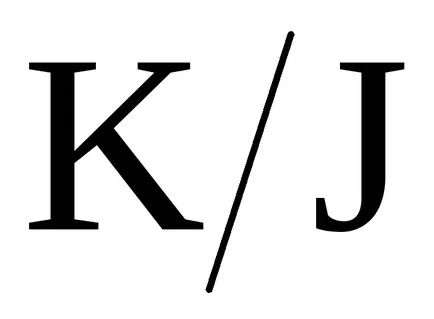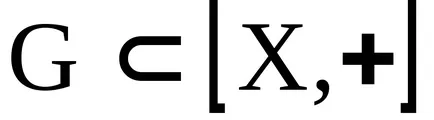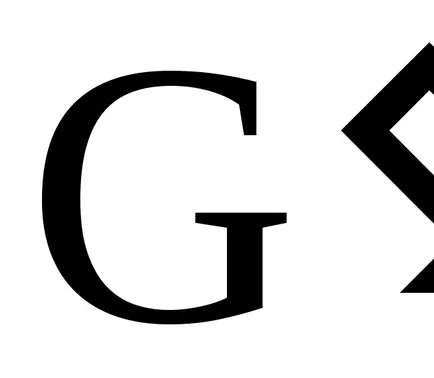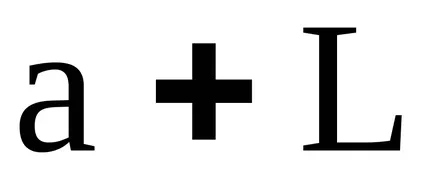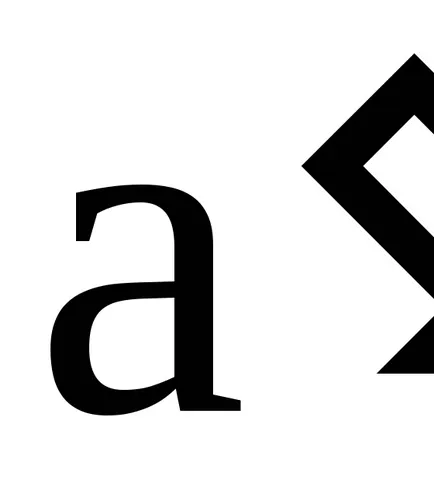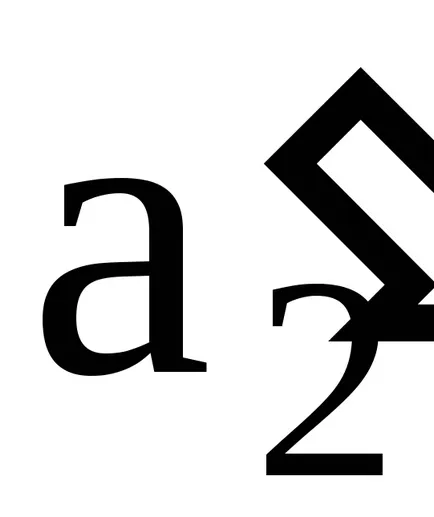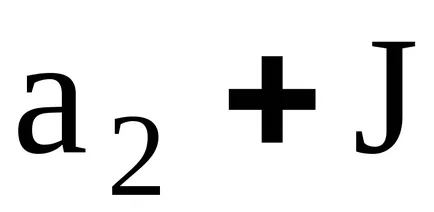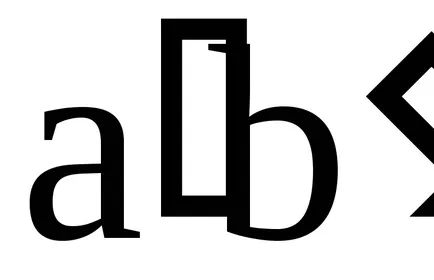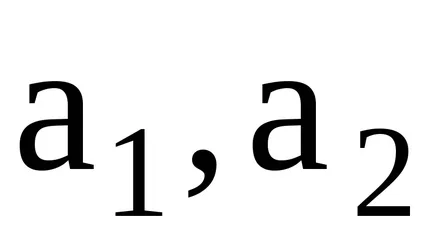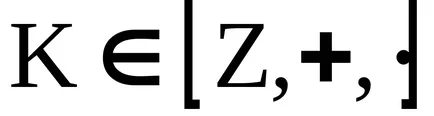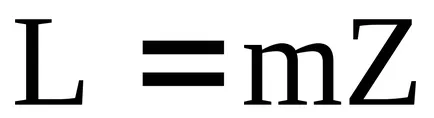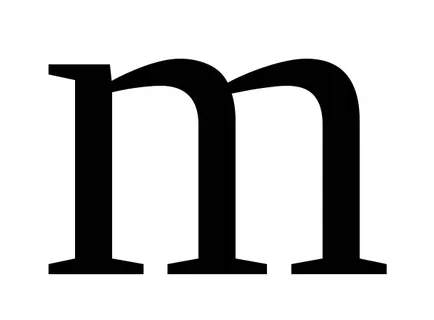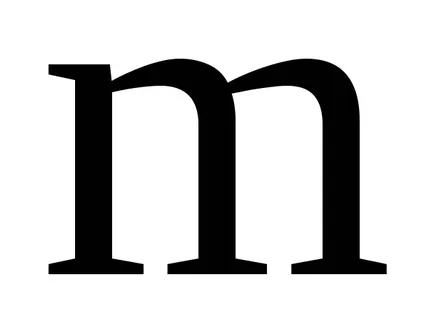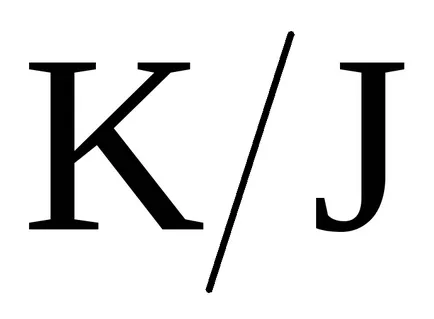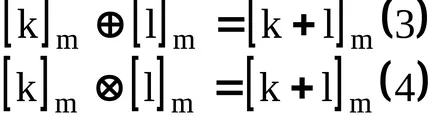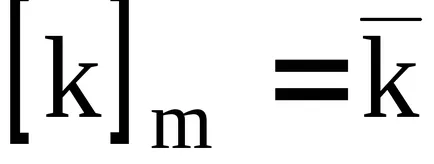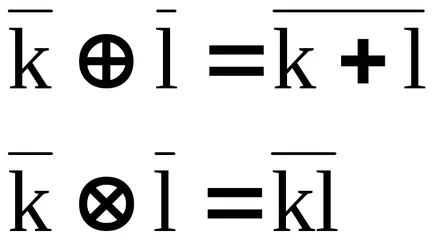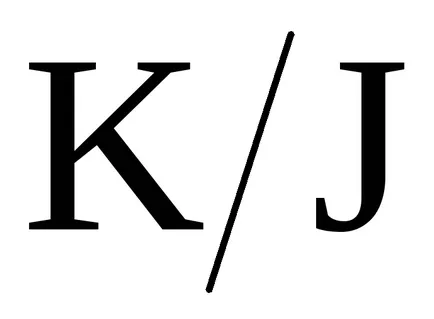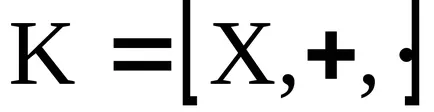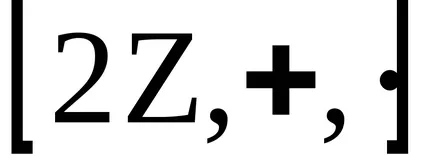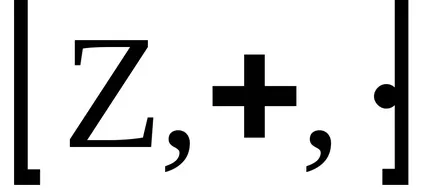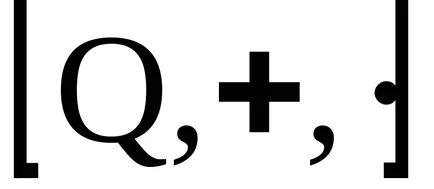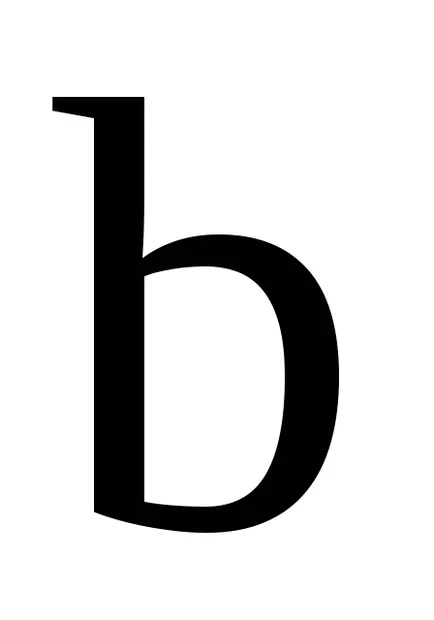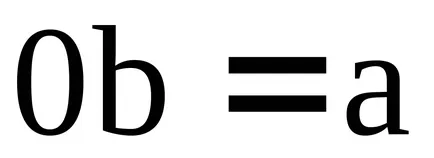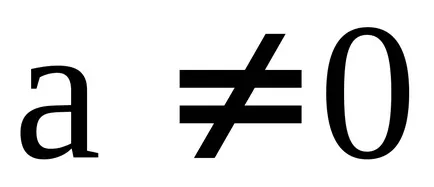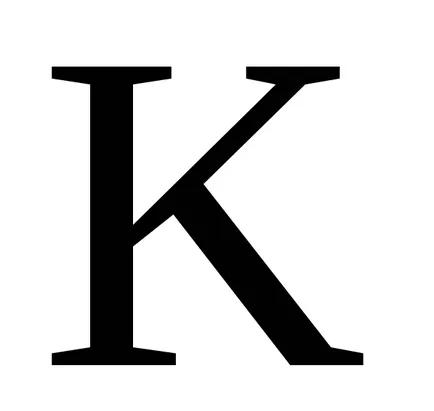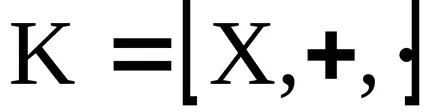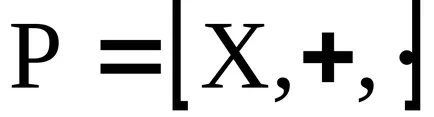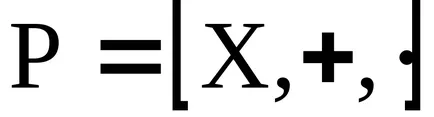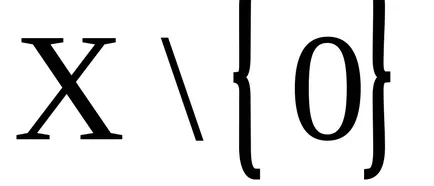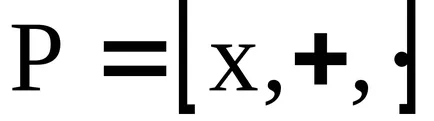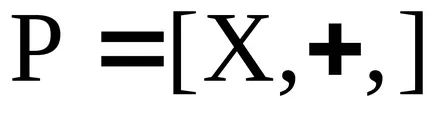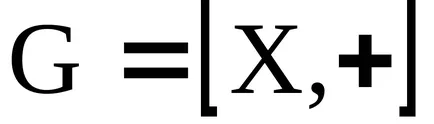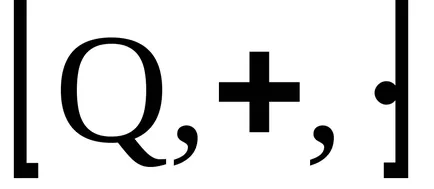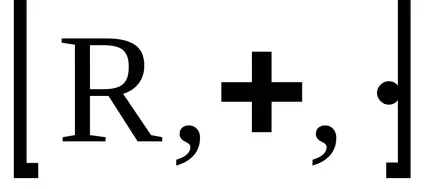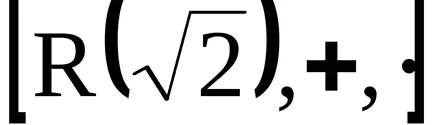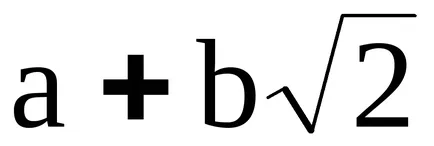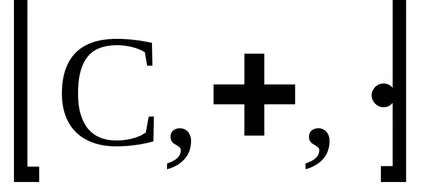A koncepció az ideális
gyűrűk
H hasonló a normál osztó csoport G. Ez a konstrukció lehetővé teszi, hogy a megközelítés a hányadost gyűrűt
ugyanolyan módon, mint az építőiparban a faktor G csoport / H.
enged
- ideális
.
Mivel a alapgyűrű
Ez egy additív Abel-csoport
, elemként hányados gyűrűk kiválasztáshoz cosets
, ahol
, amely nazyvayutsyaklassami maradékok modulo egy gyűrű ideális.
Tétel. A több adalékanyag cosets
alaktényező gyűrűt
A műveletek:
Ezen túlmenően, az a természetes térkép vidayavlyaetsyaepimorfizmom (
- szürjektıv).
Bizonyítás. A Abel-csoport
bármely alcsoportja
normális, mert , Ezért az expressziós (1) meghatároz egy Abel-csoport hányadost gyűrűt, és a leképezés rá additív Abel-csoportok G és
.
Továbbra is ellenőrizheti, hogy a kifejezést (2) egyértelműen meghatározza a szorzás a sor adalék cosets
, azaz Ez nem függ a választott képviselőinek az osztályok.
enged
,
- képviselői a két cosets
és
, azaz
,
,
Továbbra is azt mutatják, hogy
.
Sőt, mivel
és
- ideális K, akkor
ezért
Ezek az azonos mellékosztály elemekkel
, ami azt jelenti, hogy a termék (2) igaz.
Példa. Tekintsük a gyűrű egészek
. Az ideális az, hogy a gyűrű
, azaz az egész számok osztható m nyom nélkül.
Adalék a gyűrű szomszédos K osztály ideális
Ez a forma, ahol.
A több cosets adalék pontosan
maradék osztályok modulo
, és megvan a forma:
Így, a gyűrű alakú elemek a faktor
a maradék osztályok modulo
.
művelet
, A faktor koltsezadayutsya a maradék osztályok, mint a múltban:
,
akkor fix m, mint eddig is, hogy használja a gyors-
:
A koncepció a gyűrű-faktor
Az ideális gyűrű
Ez lehetővé teszi, hogy az alapvető tétel a homomorfizmus gyűrűk.
A mező meghatározása, egysejtűek tulajdonságait.
Bármely gyűrűben
kivonás végzik - az inverz művelet hozzáadás:
A műveletek végrehajtása során a részleg - az inverz művelet a szaporodás a meghatározása a gyűrű nem mond semmit. Belátható, hogy tekintettel a osztási művelet különböző gyűrűk rendelkeznek különböző tulajdonságokkal. Például, a gyűrű páros számok
elosztjuk egy számot egy másik végzik csak kivételes esetekben; hogy gyűrű nincs olyan elem, amely osztozik annak minden eleme.
A gyűrű az egészek
felosztása egy szám egy másik végezzük kivételes esetekben, de minden eleme a gyűrű osztva 1 és -1. A gyűrű racionális
osztás mindig megtörténik, kivéve nullával osztani.
Megjegyzés. Osztás nullával lehetetlen bármilyen gyűrű: osztott elem
0 - azt jelenti, hogy megtalálják egy elemet a gyűrű
, hogy
, de amikor
ez nem lehetséges, mert minden eleme a gyűrű
:.
A magasabb algebra különösen a matematika általában speciális szerepet játszanak kommutatív gyűrű. Ez végre, amelyben osztás mint nullával osztani. Ezek az úgynevezett területeken.
Adunk több meghatározása terén, amelyek tükrözik a főbb jellemzői.
Opredelenie1. kommutatív gyűrű
nazyvaetsyapolem és jelöljük
, ha tartalmaz legalább egy elemet nullától eltérő, és ha ez végre egy osztási művelet, mint osztás nullával, vagyis a valamennyi elemének
és
, amelyből
, tartalmaz egy és csak egy ilyen elem
, hogy
:
elem
Ez az úgynevezett privát elemek
és
és meg van írva, a frakció.
Opredelenie2. Paul
kommutatív gyűrű, amelyben nonzeros
csoportot alkotnak a működését szorzás:
multiplikatív csoportjában egy mező.
Opredelenie3. mező
- kommutatív gyűrű egységét nem egyenlő nullával, ahol mindegyik nullától eltérő elem invertálható:
Mint látható a definíciók terén
Ez egy hibrid a két csoport - additív Abel-csoport
és multiplikatív kapcsolódó elosztó törvény (jelenleg egy, a kommutativitás).
Megjegyzés. Foglalt követelmények meghatározása terén nevezzük axiómák terén.
Definíció. Térelemek számok, az úgynevezett numerikus mezőket.
1. A gyűrű a racionális számok
Ez egy területen.
2. A gyűrű a valós számok
Ez is egy területen.
3. Ring
szám az űrlap
, ahol
, Ez egy területen.
4. A gyűrű a komplex számok
Ez egy területen.
Az összes példa numerikus mezőket. Példák a nem-numerikus mezőket az alábbiakban tárgyaljuk.