Előadás 2 (chislo_e)
Tétel 2. A szekvencia
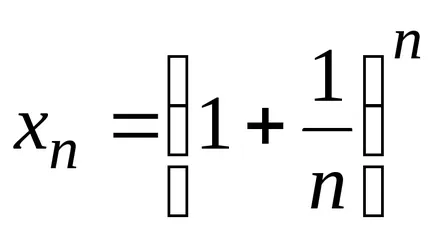
Bizonyítás. 1. Tekintsük a kiegészítő szekvenciát
Megmutatjuk, hogy konvergál. Így használjuk a határ egy monoton sorozatot. Vegye figyelembe, hogy yn> - korlátozott, mivel a lemma Bernoulli
,
Továbbá alulról korlátos száma 2.
2. Lássuk be, hogy a (2) nem növeli, erre meg egy bizonyos:
.
kaptunk
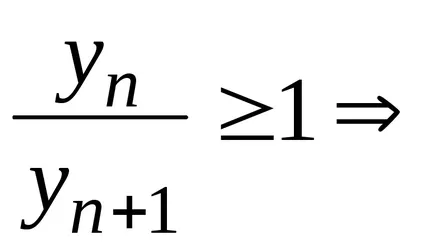
Ennek alapján 1-2 következtetni, hogy (2) konvergál.
Megjegyezzük, hogy
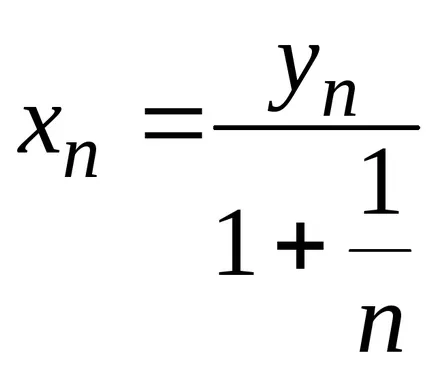
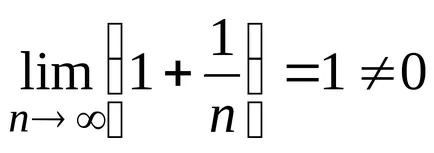
Megjegyzés: 1. Euler (svájci matematikus 1707-1783), amely szám a határ sorozatából
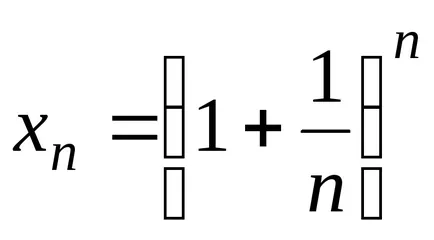
e = 2,718281828459045. - irracionális szám t arr ..
2. megjegyzés: Ha a szám e vzyats logaritmus alapja, mint a logaritmus az úgynevezett természetes logaritmus és ln abaznachayut. Ennélfogva, a meghatározás lnh = logex.
