Építése felületek Mathcad és juhar
Mathcad. Építése felületeken.
Gyors építése a legegyszerűbb módja annak, hogy építsenek felületeken. Ehhez:
1. egy lapon Mathcad írja be a képletet z (x, y): = ...;
2. Válassza ki a parancsot a főmenü „Insert”, „Schedule”, válassza ki a típus menetrend „felület” az eszköztáron „Charts”.
3. A három dimenziós grafika sablon adja meg a nevét függvény nem érvek.
Építése felületek a z mátrixban.
A legtöbb „helyes” módszert kirajzoló által meghatározott felület két változó a Z = f (x, y), az, hogy töltse ezt a funkciót mátrix értékek. Így a sorok és oszlopok a mátrix értelmezni abszcissza és ordináta. például:
Függvényt meghatározó a két változó a z (x, y): = cos (x y.)
A sorok száma ábrázolhatók és méret N: = 40 M: = 40
Meghatározása indexek i: = 0..n J: = 0..n
Meghatározása tömbök és az x-ordináta xi: =
A háromdimenziós grafika sablon, írja be a nevét a z tömböt:
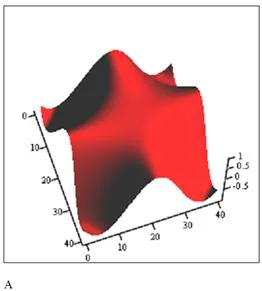
Építőipari segítségével CreateMesh funkciót.
A formátum egy függvényhívás:
CreateMesh (F. X1, X2, Y1, Y2, xgrid, ygrid, mesh).
CreateMesh funkció paraméterek:
Mesh - a sorok számát a rács funkció;
F - formájában a függvényt (vagy lehet egy általános képletű, vagy egy háromdimenziós vektort meghatározó egyes koordináta paraméteres formában, vagy három különálló funkciók meghatározó koordinátákat paraméteres alakban);
- x1 - az alsó határ az x változó;
- x2 - a felső határa az x változó;
- y1 - az alsó határ y változó;
- y2 - a felső határ y változó;
- xgrid - a pontok száma az x változó;
- ygrid - a pontok száma y változó.
A koordináta-rendszer, akkor lehet építeni egyes felületeket, ez elég ahhoz, hogy azonosítani őket, majd a menetrend a sablon meg nevüket paraméterek nélkül, vesszővel elválasztva:
Az építőiparban ugyanazon a grafikonon derékszögű, hengeres
és gömb koordináta rendszer
Legyen adott némi funkció, mint például a z (x, y) = const. A különböző koordináta rendszer, ez a funkció a különböző menetrendek. Egy derékszögű koordináta-rendszer egy sík párhuzamos az xy síkban egy hengeres - hengeres jobb forgású egy bázissal sugarú const, egy gömb alakú - labdát sugarú const. Ha módosítani szeretné a koordináta-rendszer, szükség van a minta a grafikon jobb gombbal a megjelenő listában válassza ki a „Tulajdonságok”, majd „Data QuickPlot”, és adja meg a kívánt koordináta rendszerben. például:
Az építési poliéderek a Mathcad van Poliéder funkciót. Ezt fel lehet használni kétféleképpen:
1) a neve, akkor a függvény mondjuk Poliéder ( „polyhedron neve”);
2) a kódot, akkor a függvény mondjuk Poliéder ( "# polyhedron szám").
Építése felületek a forradalom.
Az építési felületek forradalom Mathcad CreateMesh hasznos funkció.
CreateMesh funkció paraméterek:
- x1, y1, z1 - mátrix értékek minden koordináta-;
- -5 - az alsó határ a változó u;
- 5 - a felső határa a változó u;
- 0 - az alsó határ a változó v;
- 2p - a felső határa a változó v;
- 30 - a sorok számát a rács grafikonon.
A paraméteres egyenletek számára körüli forgatás az x-tengely:
Paraméteres egyenletek fordult a tengely körül Oy:
Példa: Tekintsük hiperbola y 2 - x 2 = 1. Ha ezt a forgási tengelye körül Ox hiperbola kapott hiperboloid egy lap, a forgás által a tengely körüli Oy - két-sheeted hiperboloid. Építünk forgásfelület:
Épület egy térbeli vonalak.
Vonal a térben, úgy, mint a nyoma a mozgó pont, a rendszer úgy tűnik három egyenletet: X = x (t); y = y (t); Z = z (t), kifejezetten a pont koordinátáit t. Ezek az egyenletek az úgynevezett paraméteres egyenletek térbeli vonalak. A konstrukció a tér vonalak Mathcad van egy funkciója CreateSpace.
- F - vektor paraméteres koordináta egyenletek;
- t1 - az alsó határ a változó;
- t2 - a felső határa a változó;
- tgrid - a rácsvonalak száma; opcionális paraméter; minél nagyobb az érték, annál simább a vonal kapunk; ha ez nem elég nagy, a vonal fordul megtört.
Maple. Építése felületek és térbeli vonalak.
Menetrend felület adott explicit függvénye.
lehet levonni alkalmazásával plot3d paranccsal (f (x, y), X = X1 ... x2, y = y1 ... y2, opciók). A paraméterek a parancs átfedésben a plot parancs paramétereit. Gyakran használt paraméterek közé parancsok plot3d fény = [angl1, angl2, c1, c2, c3] - feladata világítás felszíni generált pont fényforrás gömbi koordináták (angl1 angl2.). A vörös szín által meghatározott lebeny (c1), zöld (c2), és a kék (c3) a színek, amelyek a tartományban [0,1]. Paraméterkészletek style = opt rajz stílus: POINT -ponttal, LINE - vonal, rejtett - háló eltávolítása rejtett vonalak, folt - töltőanyag (alapértelmezett), Vázlatos - háló kimenetének rejtett vonalak, CONTOUR - szintvonal, PATCHCONTOUR - töltőanyag és szintig. Paraméter árnyékolás = opt állítja függvényében összevont intenzitás értéke xyz - az alapértelmezett, NINCS - anélkül, színezés.
Priver: össze egy felülete x 2 + 4Z = 4. Mivel az első erejét Z, lehetőség van, hogy kifejezzék, és hogy a funkció kifejezetten, megkapjuk, z =. Vvodimv Maple:
A (telkek). plot3d (<+ 0. y 2>, X = -5..5, y = -5..5, grid = [25,25], tengelyek = normál)
Menetrend meghatározott felület implicit.
A háromdimenziós felületi telek, hallgatólagosan a következő egyenlet adja
, alkalmazva szerkesztjük plot parancs csomag: implicitplot3d (F (x, y, z) = c, X = x1..x2, y = y1..y2, Z = z1..z2), amely meghatározza a felület egyenlete
és a méret a minta a koordináta-tengely.
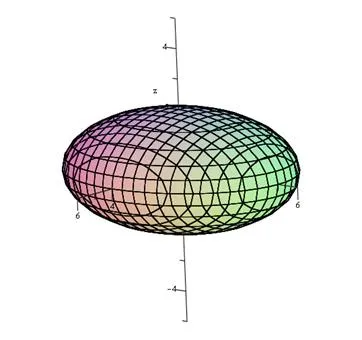
Nyilvánvaló, hogy a funkció hallgatólagosan, így használjuk a fenti algoritmusnak.
Menetrend meghatározott felület parametrikusan.
Ha szükséges, hogy létrejöjjön meghatározott felülettel parametrikusan: x = x (u, v), y = y (u, v), Z = z (u, v), majd ezeket a funkciókat felsorolt zárójelben A csapatban: plot3d ([x ( u, v), y (u, v), z (u, v)], u = u1..u2, v = v1..v2).
Példa: építeni felület parametrikusan megadva: x = 2 u + v, y = v. cos (u),
z = v. sin (u). Először, definiáljuk funkciók X0, Y0, Z0, amely megfelel a funkciók x, y, z.