Építőipari grafikonok trigonometrikus függvények - Algebra - 10 óra osztályok - összefoglalók tanulságok

Tema.Postroenie grafikonok trigonometrikus függvények

Cél: a rajzoló funkciókat y = sin x. y = cos x. y = tg x. y = CTG x.

Képződése képességek telek funkciók: y = Asin (kx + b), y = Acos (kx + b), y = Atg (kx + b), y = ACTG (kx + b).

I. ellenőrzése házi

1. Az egyik diák játszik a megoldást gyakorlat 24. szám (1-3).

2. Első beszélgetés:

1) Hívja jelenségek a természetben, hogy periodikusan ismétlődnek.

2) Adjuk meg a periodikus függvény.

3) Ha a függvény az y = f (x) az a szám, a T periódus, az időszak a függvénye lesz a száma 2T, 3 T. A indokolják.

4) meg azt a legkisebb pozitív időszak funkciók:

a) y = cos; b) y = sin; c) Y = tg; z) = y.

5) periodikus függvény y =? Ha igen, adja meg az időszak a funkciót.

II. Építése a függvény grafikonját az y = sin x

A konstrukció a grafikont a funkció y = sin x használja a készüléket kört. Construct egységnyi sugarú kört 1 cm-es (2 sejtek). Jobb össze egy koordináta-rendszer, ábrán látható. 57.

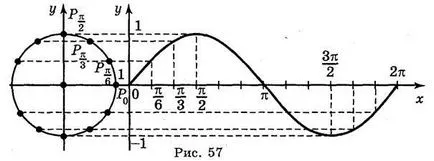
Az x tengely telek pontok; π; ; 2 π (rendre 3 sejtek, 6 sejt 9 sejteket 12 sejt). Szakaszban az első negyedévben az egység kör három egyenlő részre, és ugyanazt a darabszámot vágni az x tengely. Transzfer a szinusz érték a megfelelő pontokat OX tengelyen. Kapunk az a pont, ami kell csatlakoztatni egy sima vonal. Ezután osztani a második, harmadik és negyedik negyedét az egység kör három egyenlő részre, és át az érték a szinusz a megfelelő pont x-tengelyen. Ezt követően egymás után egyesíti az összes adatpontot, megkapjuk a függvény grafikonját y = sin x intervallumban [0; π].

Az ok, hogy a függvény az y = sin x periodikus egy időszakra 2 π. az, hogy ábrázoljuk az y = sin x a teljes vonalat OX párhuzamos elég ahhoz, hogy mozgatni ábrázoltuk az x-tengely által 2 π. 4 π. 6 π. egységet a bal és a jobb (ábra. 58).

Görbe, amely a függvény grafikonját y = sin x. az úgynevezett szinusz hullám.

1. Készítsük el a grafikonok a funkciók.

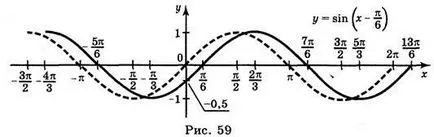
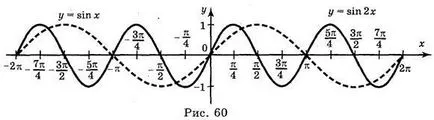
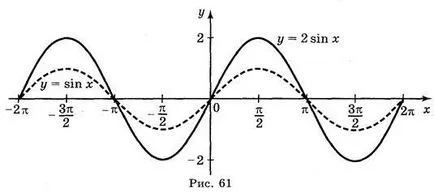
a) y = sin; b) = sin y 2; c) y = sin 2 x; d) y = sin (-x).

Válaszok: a) ábra. 59; b) ábra. 60; c) ábra. 61; g) ábra. 62.

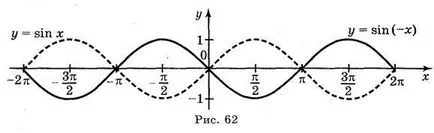
III. Építése a grafikont a funkció y = cos x

Mint tudod, cos x = sin. így = cos x és y = sin - ugyanazt a funkciót. A konstrukció a grafikont a funkció y = sin-használata geometriai transzformációk grafikonok: első konstrukcióval (63. ábra). A grafikon y = sin x. akkor Y = sin (-x), és a végén a = sin.

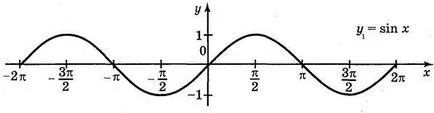
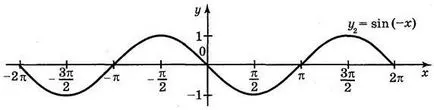
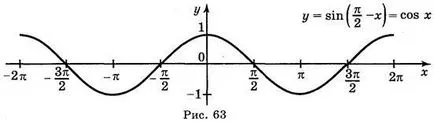
1. Rajzolj grafikonok a funkciók:

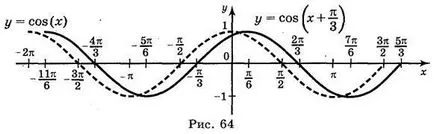
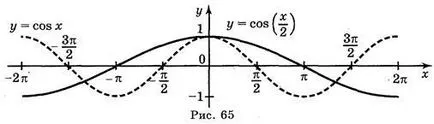
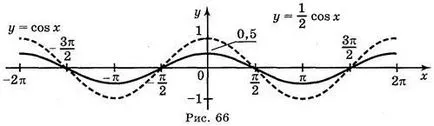
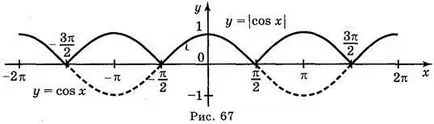
a) y = cos; b) Y = cos; a) y = cos x; g) = y | cos x |.

Válasz: a) ábra. 64; b) ábra. 65; c) ábra. 66; g) ábra. 67.

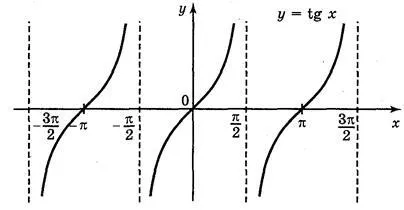
IV. Építése a grafikont a funkció y = tg x

A grafikon a függvény az y = tg x konstrukció keresztül érintő vonal időközzel amelynek hossza egyenlő a π időszak ez a funkció. Construct egységnyi sugarú kör 2 cm-es (4 sejt), és felhívni érintő vonal. Jobb össze egy koordináta-rendszer, ábrán látható. 68.

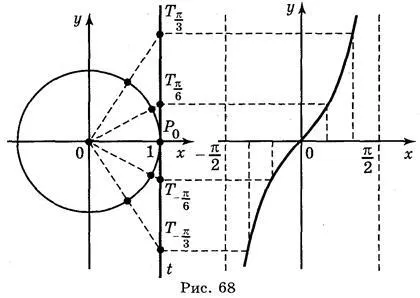
Az x tengely telek pontok; (6 sejt). Osszuk az első és a negyedik negyed kör 3 egyenlő részre, és ugyanazon a részek, és az egyes szegmensek. Keressük az értéke az érintő számok; ; 0; ; via érintő vonal (ordináta pont ;;;; érintő vonal). Transzfer az értékeket a megfelelő pontokat érintők OX tengely. Egymást követően egyesíti az összes adat pont, megkapjuk a grafikon y = tg x intervallumban.

Az a tény, hogy a függvény az y = tg x periódusidővel π, ábrázolni a függvény az y = tg x a teljes vonalat OX párhuzamos elég ahhoz, hogy mozgatni ábrázoltuk az x-tengely mentén π. 2 π. 3 π. 4 π. egységek a bal és a jobb (ábra. 69).

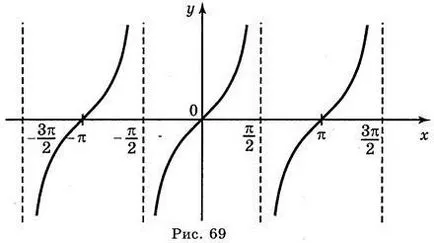
A grafikon y = tg x tangensoїdoyu nevezett.

1. grafikon funkciók

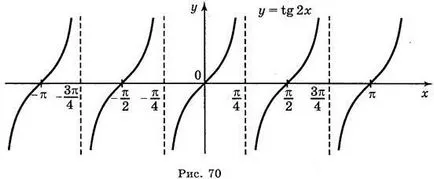
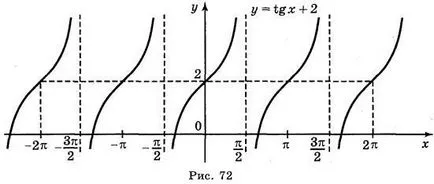
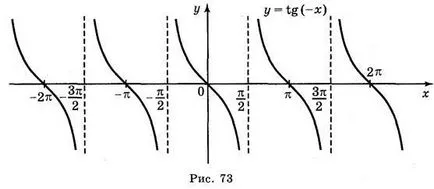
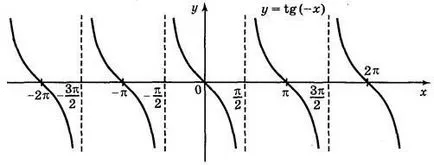
a) a TG = 2; b) Y = t g x; c) y = tg x + 2; d) y = tg (-x).

Válaszok: a) ábra. 70; b) ábra. 71; c) ábra. 72; g) ábra. 73.

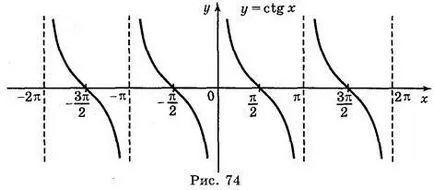
V. építése a grafikont a funkció y = CTG x

A grafikon a függvény az y = CTG x könnyen előállítható képletű CTG X = tg és két geometriai transzformációk (ábra. 74) képest a szimmetriatengely ΟΥ párhuzamos fordítás az x tengely mentén.

IV. házi feladat

§ és 6. § kérdések és feladatok ismétlés részt és számos 50-51. Vocabulary № 28 (a-d).