Exponenciális egyenletek és egyenlőtlenségek

Exponenciális egyenletek és egyenlőtlenségek

Többségi döntése matematikai problémák ilyen vagy olyan módon kapcsolódik az átalakítás a numerikus, algebrai vagy funkcionális kifejezéseket. A fenti különösen vonatkozik a döntés exponenciális egyenletek és egyenlőtlenségek. Azokban a kiviteli alakokban HASZNÁLHATÓ matematikai problémákat az ilyen típusú közé tartozik különösen, C3 feladat. Megtanulják, hogyan kell megoldani a feladatot C3 fontos, hogy ne csak a sikeresen a vizsgát, hanem az az oka, hogy ez a képesség hasznos a tanulmány a matematika középiskolában.

Mielőtt egy elemzése konkrét exponenciális egyenletek és egyenlőtlenségek. mint a tanár matematika, azt javasoljuk, hogy ecsettel fel néhány elméleti anyagot, amire szükségünk van.

exponenciális függvény

Mi egy exponenciális függvény?

Funkciója formájában y = a x. ahol a> 0, és a ≠ 1, az úgynevezett exponenciális függvény.

A fő tulajdonságait az exponenciális funktsiiy = a x:

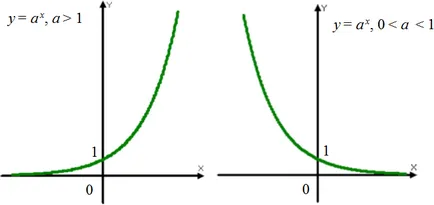
Grafikonok exponenciális függvények (exponenciális)

Megoldás az exponenciális egyenletek

Ilyenek egyenletek, amelyekben az ismeretlen változó csak szempontjából semmilyen mértékben.

Hogy oldja meg az exponenciális egyenletek tudniuk kell, és hogy képes legyen használni a következő egyszerű tétel:

Emellett célszerű, hogy emlékezzen a képletek és akciók fok:

Példa 1. egyenlet megoldásához:

Megoldás: A fenti általános képletű, és a helyettesítés:

Az egyenlet válik:

A diszkriminánsa másodfokú egyenlet kapott pozitív:

Ez azt jelenti, hogy az egyenletnek két gyöke. Keresse meg őket:

Rátérve, hogy megfordítsa a helyettesítés, megkapjuk:

A második egyenlet nincsenek gyökerei, mivel az exponenciális függvény szigorúan pozitív egész tartományban. Problémák a második:

Ezzel azt mondta, az 1. tétel pass egyenértékű egyenletet: x = 3 Ez lenne a válasz a munkát.

2. példa: az egyenlet megoldásához:

Megoldás: korlátozások körét megengedett értéke az egyenlet van, mint a radikális kifejezést értelme bármelyik értéke x (exponenciális függvény y = -x április 9 pozitív és nem nulla).

Megoldása egyenlet felhasználásával egyenértékű transzformációs szabályokat szorzás és osztás fok:

Az utolsó átmeneti végeztük összhangban 1. Tétel.

3. példa: oldja egyenletet:

Megoldás: mindkét oldalán a kezdeti egyenlet lehet osztani 0,2 x. Ez az átmenet egyenértékű lenne, mivel ez a kifejezés nagyobb, mint nulla bármelyik értéke x (exponenciális függvény szigorúan pozitív saját domain). Ezután a egyenlet:

4. példa egyenlet megoldásához:

A megoldás: egyszerűsítése egyenlet elemi egyenértékű konverziókat csökkentett elején szabályainak osztás és szorzás fok:

Elosztva mindkét oldalán az egyenlet által 4 x. Ahogy az előző példában, ez felel meg átalakulás, mert a kifejezés nem egyenlő a nulla bármely x értéknél.

5. példa az egyenlet megoldásához:

Megoldás: függvény y = 3 x. A bal oldali az egyenlet növekszik. A függvény y = -x -2/3, a jobb oldalán az egyenlet csökken. Ez azt jelenti, hogy ha a grafikonok ezen funkciók átfedik egymást, akkor nem több, mint egy pont. Ebben az esetben, ez nem nehéz kitalálni, hogy a grafikonok metszik x = -1. Egyéb gyökerek nem.

6. példa egyenlet megoldásához:

A megoldás: egyszerűsítik az egyenletet egyenértékű konverziók, szem előtt tartva mindig, hogy az exponenciális függvény szigorúan nagyobb, mint nulla minden az x és az kiszámítására vonatkozó szabályokat termék és hányadosa fok elején megadott a cikk:

Megoldás bemutató egyenlőtlenségek

Szemléltető nevű egyenlőtlenség, amelyben az ismeretlen változót tartalmazott csak a teljesítménye minden hatáskörét.

Hogy oldja exponenciális egyenlőtlenségek ismereteket igényel a következő tétel:

7. példa megoldásához egyenlőtlenséget:

Megoldás: Tegyük fel, hogy a kezdeti egyenlőtlenség formájában:

Osszuk mindkét oldalán ez az egyenlőtlenség 3 2x. ugyanakkor (mivel a pozitivitás a függvény y = 3 2x) az egyenlőtlenség jele nem változik:

Ekkor a egyenlőtlenség lesz:

Így a megoldás a egyenlőtlenség rés:

halad, hogy megfordítsa a helyettesítés, megkapjuk:

A bal oldali egyenlőtlenség miatt a pozitivitás az exponenciális függvény automatikusan történik. Használata ismert tulajdonságai a logaritmus, áttérünk az egyenértékű egyenlőtlenséget:

Mivel a mértéke alapján egy szám nagyobb, mint egy ekvivalens (2. tétel) tolódik a következő egyenlőtlenség:

Tehát végül is a választ:

8. példa megoldásához egyenlőtlenséget:

Megoldás: A tulajdonságai szorzás és hatáskörmegosztás, átírjuk egyenlőtlenséget:

Bemutatjuk az új változót:

Tekintettel a helyettesítés a egyenlőtlenség válik:

Mi szaporodnak a számláló és a nevező 7, megkapjuk a következő egyenértékű egyenlőtlenséget:

Tehát az egyenlőtlenség kielégítik a következő értékekhez t:

Ezután fordult, hogy megfordítsa a helyettesítés, megkapjuk:

Mivel az alap a ereje nagyobb, mint egy, ez felel meg (a 2. tétel) fog mozogni, hogy a következő egyenlőtlenség:

Végül eljutunk a választ:

9. példa megoldásához egyenlőtlenséget:

Osszuk mindkét oldalán egyenlőtlenség a kifejezést:

Ez mindig nagyobb, mint nulla (mivel a pozitivitás az exponenciális függvény), így nem kell változtatni a jele egyenlőtlenség. kapjuk:

Mi használjuk a változás változó:

Az eredeti egyenlet válik:

Tehát az egyenlőtlenség kielégíteni értékeit t. található a különbség:

Ami a hátsó helyettesítés azt találjuk, hogy a kezdeti egyenlőtlenség van osztva két esetben:

Az első megoldás az egyenlőtlenség nem köszönhető, hogy a pozitivitás az exponenciális függvény. Problémák a második:

Mivel az alap a teljesítmény ebben az esetben nem volt kisebb, mint egy, de nagyobb, mint nulla, egyenértékű (2. tétel) tolódik a következő egyenlőtlenség:

Tehát a végső válasz:

10. példa Döntse egyenlőtlenséget:

A parabola ágai a y = 2x + 2x 2 lefelé irányul, ezért korlátozza fent az érték, amely eléri a csúcspontjában:

A parabola ágai a y = x 2 -2x +2, állva a kitevővel felfelé irányított, így korlátozódik érték alá, amely eléri a csúcspontjában:

Együtt ez alulról korlátos, és a függvény az y = 3 x 2 -2x +2. A jobb oldalon az egyenlet. Elérte a legalacsonyabb értéket ugyanazon a ponton, mint a parabola állt az index, és ez az érték 3 1 = 3. Így a kezdeti egyenlőtlenség igaz lehet, ha a funkció függvénye a bal és a jobb szed ugyanazon a ponton érték egyenlő 3 (metszi a tartományok ezen funkciók csak egy szám). Ez a feltétel teljesül egyetlen ponton x = 1.

Ha szeretné megtudni, hogy megoldja az exponenciális egyenletek, egyenlőtlenségek, akkor kell, hogy folyamatosan a vonat a döntést. Ebben a nehéz ügyet segíthet a különböző kézikönyvek, problémamegoldás könyvek elemi matematika, gyűjtemények versenyképes feladatok osztályok matematika az iskolában, valamint az egyes ülések egy profi edző. Őszintén sikert kívánunk az előkészítés és a kiváló eredmények a vizsga.