Heurisztikus programozás, aideus
Mire a számítógépek megjelenésével szétszórt adatok pszichológia, néprajz, állat pszichológiai, pedagógiai és módszertani tudomány kimutatta, hogy az intelligencia kényelmes mind a képességét, hogy megoldja a problémákat (probléma), és a folyamat megoldások (gondolkodás) van megvalósítva a keresést egy sor olyan intézkedést indul helyzet (a feltétele a probléma), akkor le kell fordítani a végleges helyzetre (válasz). Kezdve egy bizonyos fejlettségi szintet az élő szervezetek, túl sok fellépése a tényleges végrehajtás helyébe a „virtuális” brute force „hajtogatott” akció. A matematika, abban az időben, hogy szigorú leírása helyes érvelés volt hivatalos a koncepció az algoritmus van telepítve, függően a bemeneti adatok sorrendje és leírja a probléma megoldása általánosságban. Számítógépek jött létre, mivel a készülék automatikusan elvégzi algoritmusok, azaz a. E. A problémák megoldására bemutatott szimbolikus formában. Azonban a legfontosabb kérdés marad: hogyan lehet megtalálni az algoritmusok, vagy legalább egy lineáris láncú egymást követő akciók? Mivel a NP-teljesség, sőt unsolvability általános probléma találni egy teljes lista az összes lehetőséget sok esetben lehetetlen.
Pólya szerint, az ember képes valamilyen módon leküzdeni ezt a problémát, heurisztikus - módszerek, amelyek megkönnyítik a problémamegoldás. De ez lehet programozni heurisztikus? És ha lehetséges, milyen formában kell megtörténnie? A tudósok megpróbálják megválaszolni ezeket a kérdéseket, amelynek nyomán a 1950-1960-es években, hogy a megjelenése első paradigma a mesterséges intelligencia, az úgynevezett „heurisztikus programozás”. Az AI területén a kezdetektől fogva, sok különböző kutatási területeken, de ez heurisztikus programozás lehet leírni, mint az első kísérlet arra, hogy hozzon létre egy valóban általános elmélet mesterséges intelligencia.
A heurisztikus programozási feladat mesterséges intelligencia gyakran tanulmányozta a példa a szellemi játékok, mint a dáma, sakk, t. D. Egyrészt, a „világegyetem” bármely asztali játék kap egy kis sor nagyon egyszerű szabályokkal, amelyek könnyen programozható. Másrészt, a játék során, mint a sakk, minden bizonnyal meg kell gondolni. Feladatok bizonyítani matematikai tételek és tervezési feladatokat is széles körben vizsgálták heurisztikus programozás, de szükség további domain tudás (például megmagyarázni az emberi jogok, a játék a sakk sokkal egyszerűbb, mint a szabályok integráció), és kevésbé voltak demonstratív és bonyolultabb végrehajtani. Próbáljuk meg először gondol a probléma egy egyszerű játék.
A következő megfontolások tűnhet triviális annak a ténynek köszönhető, hogy egy jól ismert és kifinomultabb módszereket. De képzelje el, azon a helyen, az úttörők, ami semmi még nem volt ismert, és ez sehol sem volt kölcsönkérni kész megoldást. Ez segít, hogy jobban megértsük az okokat és a fejlesztés területén a heurisztikus programozás és a mesterséges intelligencia kutatások általában. Sőt, többek között a szokásos kész megoldásokat lehet több véletlenszerű és nem optimális, és ezért jó ötlet, hogy vizsgálja felül a régi eredmények szélesebb összefüggésében modern ötleteket.
Legyen a mi feladatunk az, hogy tanítani egy számítógép játszani egy szellemi játék - „amőba játék” a 3 × 3. Hogyan oldja meg ezt a problémát?
Az első kívánságom, hogy határozza meg kifejezetten, hogy mi mozgatja, hogy ezt a számítógépet. Mind a kezdő általában menni ezen az úton, mert úgy tűnik, a legegyszerűbb és ellenőrzött. Hagyja, hogy a számítógép lejátssza a kereszt. Akkor egyértelműen meg kell határozni, hogy az első lépés történt a mező közepén. Ezután azonban a számítógép válasza kell függenie játékos köre.
Jelöljük a négyzetek a tábla a „sakktábla” stílusú: A1-C3. Akkor ez a játék algoritmus (C ++ szintaxis) a következőképpen néz ki
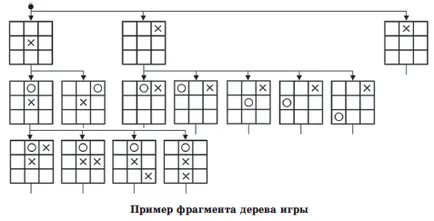
Ez az algoritmus hasonló a rendszer egyszerűen reflexek. De hol vannak a lépéseket rögzíti a programban? Annak érdekében, hogy egy bizonyos során eredményeink nyerni, akkor ellenőrizni kell az összes lehetséges mozog az ellenség. Ezt is képviselteti magát, mint egy fa játékok, más néven a fa a lehetőségek nem játék feladatokat. Az alábbi ábra egy példát mutat fragmentum fa játék „amőba játék” Field 3 × 3. A gyökér a fa egy üres tábla, és ágak induló abból megfelelnek a lehetséges stroke az első játékos. Ezek az ágak vannak az új állam a játék világban, amelyek mindegyike szintén figyelmen kívül hagyja az ágak megfelelő megengedett mozog a második játékos, és így tovább. Abban az esetben, nem játék feladatokat a gyökér a fa az opciók lehetnek például az egyenlet megoldásához, ágai kompatibilis lesz a megengedett műveletek az átalakulás ez a kifejezés.
Tény, hogy egy ilyen fa állapotát írja le térben - egy olyan feltételrendszer, amely lehet néhány, mint például a játékok világában lehetséges átmenetek állapotok között. Egyes problémák, ezt a helyet is meg lehet határozni kifejezetten felsorolja az összes lehetséges állapotok és átmenetek között, de gyakrabban adják hallgatólagosan - a szabályok formájában (játékok, integráció, stb ...). A szabályok alapján lehet megszervezni generatív eljárást kifejezetten az épület egy fa lehetőségeket.
Használjuk ezt az eljárást, hogy építsenek egy játék fa, és megtalálja benne azt válaszolja, hogy vezetne
a győzelem, vagy ha ez nem lehetséges, a döntetlen. Nekik be kell vinni a programot. Lehetséges, hogy a számítógépes program, amely lejátssza a „tic-tac-toe”, ő építette a fa lehetőségek alapján az ismert generáló eljárást? Természetesen sokkal elegánsabb (mint fent látható), és az algoritmus a saját a játék építeni a fát, és válassza ki a legjobb persze, mint mi.
Elvégzi az építési nélkül tárolható a memóriában egy további példányt a játéktér (mint az általánosabb esetben - a modell a világ) problematikus. Tegyük fel, hogy a területen [3] [3] - egy kiegészítő tömb 3 × 3, az érték, amelynél a cella van állítva „-”, amennyiben a megfelelő cella nem foglalt, és az „X” és az „O”, ha van egy „kereszt” és „toe” volt. Ezután a generáló eljárást felírható a következő formában:
Ha az előre beállított minden érték a tömb mező üres ( „-”), majd futtassa ezt az eljárást tree_ keresési ( „X”), a munkája során egy sor területen fog fordulni minden lehetséges helyen amőba játék.
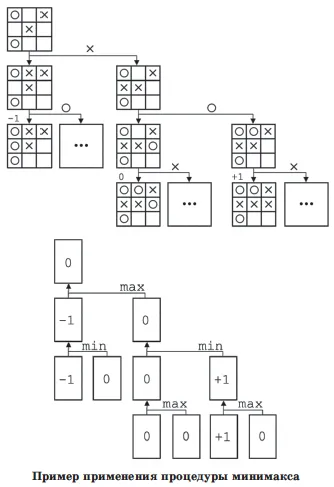
Legyen check_game eljárás, amely értékeli a helyzetet a fedélzeten, visszatérve az „X” vagy „Névjegy”, ha az egy sorban 3, vagy szállítani a megfelelő játékos „-” ha ez nem. tudjuk meg az állapotát, hogy a fa levelei (valaki nyer vagy döntetlen).
Most tekintsük a facsomópontok közvetlenül megelőző levelek. Ha legalább egy a levelek vezet nyerő játékos, melynek során megfelel az aktuális csomópont, akkor a csomópont is a győztes. A csomópont lesz vesztes csak akkor, ha a levelek, amelyben vezet, amelyek az elveszett. Ily módon, akkor jelölje meg az összes csomópont, hogy megelőzik a levelek, és továbbra is terjed az információkat le a gyökér.
Ez sokkal kényelmesebb, hogy bemutassa a számítógép erősítést „1” dolgozzon „0”, és a számítógép veszteség „-1”. Aztán, hogy meghatározza az oldal a számítógépes tanfolyam állapotát, meg kell, hogy vegye a maximumot, és az elért az ellenség - legalábbis a gyermek csomópontok. Ez az eljárás csomópontok állapotának értékelések azt az alábbi ábrán, az úgynevezett Minimax eljárás. Beágyazása a minimax eljárást generáló eljárás nem nehéz.
Meg kell jegyezni, a létezését játékelmélet, az általánosabb fogalom - a Nash-egyensúly megfelelő ilyen stratégiák a játékosok, ahonnan egyikük sem nem nyereséges eltérni, ha nem teszik a többi játékos.
Ha a termelő eljárás ismert és a minimax eljárást annak megállapítására, hogy a legjobb persze, mi a probléma? Mint már többször fentebb említettük, a probléma - az NP-teljesség. Más szóval, a teljes verzió a fa tud nagyon nagy: gyakran a csomópontok száma exponenciálisan nő a mélység a fa, hiszen minden csomópont vezet számos új egységek, amelyek mindegyike viszont ismét vezet számos új egységet. Például, a méret a fa darabok 10 ^ 40, a sakk - 10 ^ 120, és az első és elég elképzelhetetlen száma - 10 ^ 400. Ironikus, gyakran hangsúlyozni a nagysága ezeket a számokat mondani, hogy alapvető fölénye az atomok számát, vagy az elemi részecskék a világegyetem, nem teljesen indokolt, hogy összehasonlítjuk az objektumok száma, és a kombinációk száma az államok a tárgyakat. Ez az összehasonlítás azonban válik indokolttá, amikor a klasszikus rendszerek tömeges párhuzamosság: akkor is, ha minden atom az univerzumban lenne egy külön processzor, fogás 10.100 kombinációk másodpercenként, az egész univerzum minden idő telt el a Nagy Bumm óta, nem elég játszani egy tökéletes játék a második.
Fa megadott lehetőségek implicit módon, a játékszabályok, egyfajta láthatatlan a programot. Amint a patkány, hogy vizsgálja meg az igazi labirintus, meg kell tölteni egy kis időt a tanulmány egyes villa, majd folytatódott az útvonal nem látható, és a programot kell tölteni egy kis időt (számítási erőforrások), hogy vizsgálja lehetőségeket a fát, és megtalálni az utat a győzelemhez.
Annak ellenére, hogy a látszólagos elemi játék „Tic-Tac-Toe” még a 3 × 3-egy gyermek, aki nem ismeri, csak jelentős szellemi erőfeszítést. Ez a játék megköveteli a keresési változatok mélységben 4-5, ami közel van a megállapítása összetett közepén a szegmens feladatok segítségével egy vonalzó és iránytű. Azonban a „gondolkodás” egyszer „tic-tac-toe” a 3 × 3-as, tudni fogjuk a döntést (az út a „labirintus” opciót), és a játék elveszti érdeklődését. A „felnőtt” szellemi játékok ilyen korlátozások nem jellemző, mert az összes keresési tér bennük nem lehet vizsgálni, az egész egy ember életét, sőt az egész időszak alatt a lét a civilizáció.
Mit lehet tenni, ha az egész fa keletkezik nem lehet? Mi az oka, hogy válasszon egy tanfolyamot? A heurisztikus programozás, a „heurisztikus” mezőben van megadva, mint egy eszköz, amely lehetővé teszi, hogy csökkentsék a rendezési lehetőségek ígérő ágak a fán, amely sokkal pontosabb meghatározására, mint a két heurisztikus módszerekkel megkönnyítve a megoldás a problémára.
A heurisztikus már hallgatólagosan elkészítéséhez használt a játék fa „Amőba”. Ez azt mutatja, az összes kezdeti játék pozíciókat, nem egymásba forgatás és tükrözés. Más szóval, a heurisztika használt szimmetria. Hány változata a játék, ha nem veszi figyelembe a szimmetria? Számuk - nem több, mint faktoriálisát száma 9. Az szimmetriák száma csökken, amely sorrendben. Ugyanakkor a relatív nyereség nagy területeken is sokkal kisebb, mint már ezt követően több stroke szimmetrikus folytatása megszűnnének.
Symmetry egy nagyon általános heurisztikus, de nem túl erős, mert a szimmetria a játék helyzetet (akkor is, ha van ilyen), nagyon gyorsan megtört.
El lehet képzelni egy bonyolultabb (és magán) heurisztikus: a jövedelmezőbb a lépés, hogy potenciálisan felhasználható egy nagyobb számú konstrukciók három egy sorban. A viszonyítási alap heurisztikája „kereszt” a leginkább jövedelmező lépés, hogy a központban, mert részt vesz négy különböző konstrukciók. Aztán ott vannak még a sarkokban - számukra száma szerkezetek három. Mozog, a falakon ez a szám csak kettő. Nyilvánvaló, hogy ennek a heurisztikus nem elegendő, mert figyelmen kívül hagyja az ellenség képességek (például, teljes annak kombinációja).
Ez természetes vágy, hogy értékelje a nyereségesség a haladás mennyiségileg. Az ezeken alapuló mennyiségi vágható rész ágak minden egyes csomópontnál a fa erre. És valóban, a heurisztikus heurisztikus programozási feladata formájában (statikus) függvény kiértékeli a leggyakoribb.