Hogyan lehet megoldani a problémát a sebesség a folyó
Amellett, hogy a problémát a mozgás sebessége általában egységes és egyértelmű, és ismertetik egyszerű egyenletek. Ezek a problémák azonban tudható, hogy a legnehezebb problémákat a mechanika. A fenti problémák megoldására az a szabály felül a klasszikus árak. Ahhoz, hogy megértsük az elvet a megoldás, akkor jobb, ha úgy vélik, hogy konkrét példákat problémákat.

oktatás
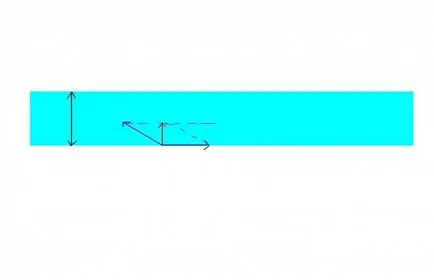
Egy példa a szabály hozzáadás sebességét. Hagyja, hogy a folyó áramlási sebesség v0, és a sebesség a hajó, úszott a folyón, a víz viszonylag v1 és merőleges a partra (lásd 1. ábra). Hajó egyidejűleg részt vevő két független mozgás: ez egy ideig t úszik folyó szélessége H képest sebességgel v1 w vizet, és ugyanabban az időben fúj downstream egy L távolság. Ennek eredményeként, a hajó lebeg S úton sebességgel v viszonyítva th partján modulus: v egyenlő a gyökér a expressziós kvardratny V1 négyzetes + V0 a négyzet a időben t. Ezért tudjuk írni az egyenleteket, hogy megoldja a hasonló problémák: H = V1T, l = v0t? S = a négyzetgyökét kifejezések: v1 négyszögletesre + v0 négyszögletesre, szorozva t.
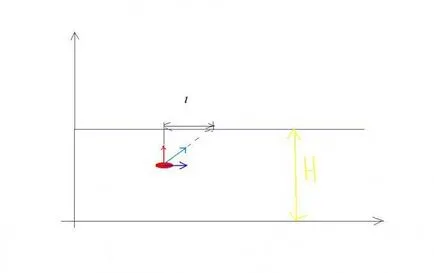
Egy másik típusú ilyen problémák kérdéseket: milyen szögben a szárazföldi sor evezős a csónak, hogy a másik oldalon, amelynek legkisebb átkelés közben az út? Egy ideje, ez az út vége lesz? A motorcsónak-én át ezen a módon? E kérdések megválaszolásához kellene egy rajz (lásd 2. ábra). Nyilvánvaló, hogy a legrövidebb út, amely akár egy hajón folyón, a folyó szélessége egyenlő az N. Vitorlázni Ily módon, a evezős kell irányítani a hajót szögben úgy, hogy Brega amikor Kotormo vektor abszolút sebessége v a hajó lesz merőleges a parton. Ezután a derékszögű háromszög, megtalálja: cos a = v0 / v1. Ebből tudjuk levezetni a szög. Speed meghatározni az azonos háromszög a Pitagorasz-tétel: v = négyzetgyök kifejezések: v1 négyzeten - V0 kvadrate.I végre ideje t, amelyre a csónak a folyón szélessége H, mozgó második sebességgel v, t = H / v .
A probléma az skorostreki „class =” lightbx „adat-gyűjtőbe =” cikk-kép „>