Kísérleti meghatározása molekuláris sebességek
Kísérletek sebességének meghatározására molekulák bizonyult érvényességének képletű (4.7.3). Az egyik kísérletet végeztünk a német fizikus O. Stern 1920
A kísérleti elrendezés ábra mutatja 4.15. A készülék tartalmaz egy 1 hajót, a rendszer a membránok 2, 3 és 4 henger forgó nagy szögsebességgel.
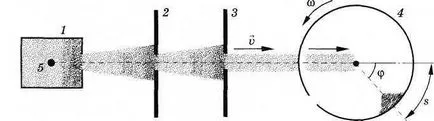
Az 1 edényt kifeszített vékony platina huzal 5 bevonva egy réteg ezüst. A vezeték elektromos áramot vezetünk. Amikor az aktuális réteg ezüst bepároljuk, és a hajó gázzal van feltöltve ezüst atomok. A gáz az egyensúlyi állapotban hőmérsékleten T, amely mérhető.
A tartály fala 1 van egy kis lyuk, amelyen át egy kis mennyiségű ezüst atomok repül ki a tartály egy térbe, ahol a nagy vákuum jön létre. Itt az atomok nem ütköznek egymással.
A zárólemezek 2, 3 van allokálva egy gerendát atomok irányított átmérője mentén a forgó henger. A henger egy szűk résen. Abban a pillanatban, amikor a rés a az elektronnyaláb pályája mentén, egy kis része atomok esik a henger és mozog, hogy a szemközti falra. Távolsága megegyezik a henger átmérője D, a repülő atomok során
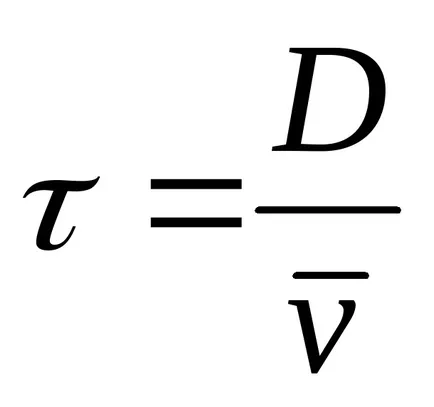

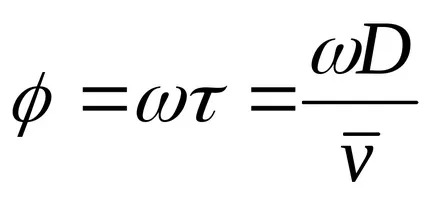
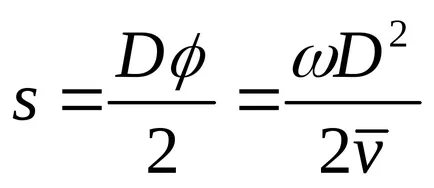
A belső felületén kialakított henger a nyoma ezüst kicsapódott formájában sötét foltok. folt vastagsága nem mindenütt egyforma. Egy bizonyos részét a maximális vastagsága az ezüstréteg. Mérése az ív hossza s, a megfelelő maximális vastagsága az ezüstréteg, és ismerve az átmérője a henger és a szögsebesség, lehetséges, hogy meghatározzuk az átlagos molekulák sebessége a következő képlet szerint:
Egyetért az érték a közepes négyzetes sebesség képlettel számítjuk ki (4.7.3), ez elég kielégítő. Ez a kísérleti bizonyítékot a érvényességét (4.7.3), és így a kifejezés (4.5.5), ami arra utal, hogy az átlagos kinetikus energia egyenesen arányos az abszolút hőmérséklettel.
Vastagságának mérésére az ezüst foltok különböző helyeken, akkor lehet számítani a atomok száma megközelítőleg a sebesség fekvő különböző időközönként. Így végre kísérleti igazolása a Maxwell eloszlás a sebesség. A megállapodás kísérletet a Maxwell-eloszlás is kielégítő.
Az átlagos sebessége egy Brown részecske
Formula (4.7.2) lehetővé teszi számunkra, hogy megértsük, hogy miért a intenzitása Brown-mozgás emelkedésével folyadék hőmérsékletét és a növekedésével csökken részecske tömege. Miután egy Brown részecske részt vesz a termikus mozgás a molekulák. Ezért, annak átlagos mozgási energiát is képlet definiálja (4.5.5) és az átlagos négyzetes sebessége - általános képletű
ahol TB - a tömeg a Brown-részecske. Ha a részecskék tömege nagy, az átlagos sebesség a mozgás annyira kicsi, hogy a mozgás egy részecske szinte lehetetlen kimutatni.
Brown részecskesebesség a folyadékban nem mérhető közvetlenül, mert a szélsőséges szabálytalanság Brown-mozgás.
Átlagos molekuláris sebessége meghaladja a hangsebesség, és eléri a több száz méter 1. Ezek a sebességek voltak képesek mérni, mivel a makroszkopikus testet (henger a Stern) lehet jelenteni, mint nagyobb szögsebessége, hogy közben a folyosón a molekulák a henger belsejében forog egy számottevő mennyiségben.