Kompatibilis lineáris egyenletrendszer
mátrix vektor algebra egyenlet
Adott egy lineáris egyenletrendszer. Bizonyítsuk be együtt, és oldja meg a két módja van:
a) Cramer-módszer;
b) útján a mátrix fogkő.
Megvizsgáljuk a kompatibilitását a rendszerben:
Az általunk használt tétele Kronecker-Capelli, erre találunk a rangot a kibővített mátrix rendszer és rangsorolja a rendszer mátrix.
Itt kibővített mátrix rendszer Echelon formában elemi transzformációk, és határozza meg a számát nem nulla sorok a mátrixban.
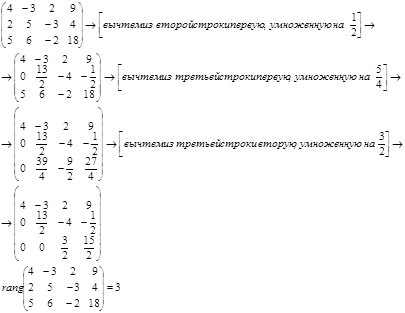
Hagyja mátrix rendszer Echelon formában elemi transzformációk, és határozza meg a számát nem nulla sorok a mátrixban.
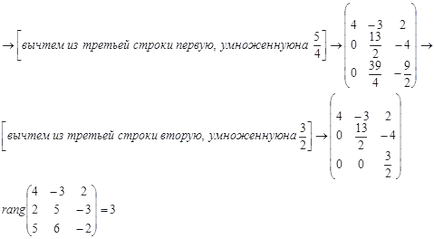
Mivel a rangot a rendszer megegyezik a rangot a kiegészített mátrix, akkor a rendszer következetes.
Keressük a megoldást a rendszer a Cramer szabály:
Mi írja le a alapmátrixához a rendszert, és megtalálja a meghatározó:
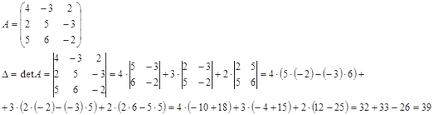
Ennek fogalmi fő mátrix rendszer (a fő meghatározója) nem nulla, akkor a rendszer egy közös.
Helyettesítsük a döntések a oszlop az első oszlopban a fő mátrix és megtalálja a meghatározó:
Mi helyettesíti oszlopon döntések a második oszlopban a fő mátrix és megtalálja a meghatározó:
Helyettesíti az oszlop készítés a harmadik oszlopban a fő mátrix és megtalálja a meghatározó:
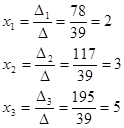
Keressük a megoldást egy mátrix módon:
Találunk az inverz mátrix. Keressük a faktorok:
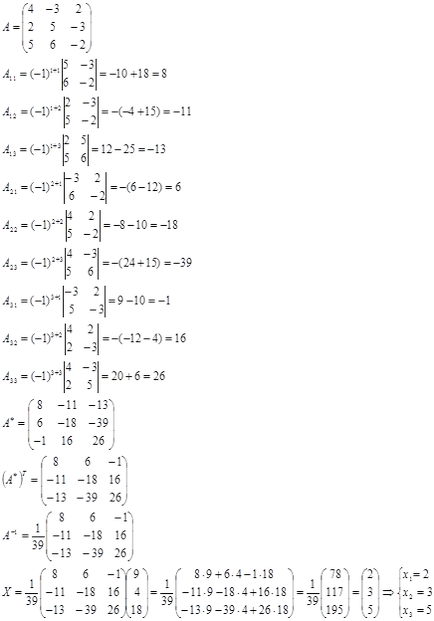
Mivel koordinátáit csúcsai egy piramis. Eszközei vektor algebra találjuk:
2) közötti szög a bordák és a;
3) a területet, az arc;
4) A kötet a piramis;
Találunk A1 A2 élhosszúságú formula
A B szög a szélek között A1 A2 A1 A4, és egyenlő a közötti szög vektorok és. Mi megtaláljuk a koordinátákat ezen vektorok:
Ezután a B szög arányából határozzuk meg az
3) Find a vektor termék
Ezután a terület az arc A1 A2 A3
4) Find a kevert termék
Ezután a hangerőt a piramis:
Bizonyítsuk be, hogy a vektorok lineárisan függetlenek, és segítenek megtalálni a terjeszkedés a vektor alapján vektorok.
Alkotunk a mátrix a koordinátákat a vektorok és határozza meg a rangsorban. Ahhoz, hogy ezt elérjük, csökkenti, hogy a háromszög alakú.
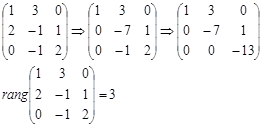
Helyezett vektor rendszer 3. A vektorok lineárisan függetlenek, és hárman, és mivel azok háromdimenziós, ezek alapját képezik a háromdimenziós térben. Bármilyen vektortérnek bővíthető a vektorok a rendszer.
Találunk koordinátáit bomlás. Mi helyettesítheti a koordinátákat a vektorok az utolsó egyenlőség.
Mivel a vektorok egyenlő, akkor a koordinátái egyenlő.
A rendszer három lineáris egyenletek három ismeretlennel. megoldani
A bomlás a vektor (6, 12, -1) ebben a alapján a formája
Adott három, a háromszög csúcsait.
a) egyenlet AB oldalán;
b) a hossza a oldalán a nap;
c) az egyenlet magassága leeresztett egy csúcsából;
d) egy olyan rendszer az egyenlőtlenségek, amelyek meghatározzák az ABC háromszög.
a) az egyenlet bal oldalát, mint az egyenlet AB találni áthaladó vonalon két pontot:
b) A hossza a BC oldalon találjuk a távolság az aktuális B és C:
c) Magasság - a vonal áthalad a pont, merőleges egyenes BC. Keressük az egyenes egyenlete BC és irányvektor:
Ekkor az egyenlet magassága:
g) egy olyan rendszer felállítása lineáris egyenlőtlenségek, amelyek meghatározzák egy háromszög. Annak megállapításához, a jel az egyenlőtlenség bal oldalán minden egyenletek két ellentétes oldalán helyettesítő csúcsainak koordinátáit, amely tartozik az adott félsíkon garantált.
Behelyettesítve a C pont (0, 5) egyenletbe AB oldalára:
Behelyettesítve a B pont (18, 8) be AC oldalán:
Behelyettesítve a pont (12, 0) az alábbi egyenlet adja oldalán BC:
Így írunk a szükséges egyenlőtlenségrendszer:
L'Hospital-szabály nem találni határait funkciókat.
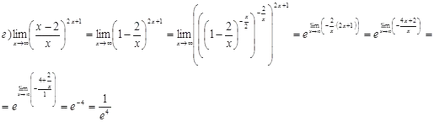
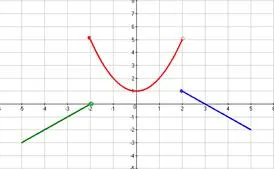
Keresse függvény break pontot, ha vannak ilyenek, az ugrást minden pontján a különbség, és létrejönne egy ütemtervet.
A domain a szakaszonként - ez az unió minden alkatrészével együtt. Így
Nyilvánvaló, hogy mind a három funkció folyamatos, megfelelő időközönként, így ellenőrizni fogjuk a határ pont.
Azt vizsgáljuk folyamatossága x = -2
- funkció határozza meg az adott ponton
Találunk az egyoldalú határértékek:
Egyoldalú határértékek végesek, és különálló, majd az f (x) van egy elsőrendű diszkontinuitás a folytatásban a ponton x = -2.
Számoljuk egy ugrás diszkontinuitás mint a különbség a jobb és bal határok:
azaz grafikon emelkedett legfeljebb 5 egység.
Annak vizsgálatára, a folytonosság a pont x = 2.
- funkció határozza meg az adott ponton
Találunk az egyoldalú határértékek:
Egyoldalú határértékek végesek, és különálló, majd az f (x) van egy elsőrendű diszkontinuitás a folytatásban a ponton x = 2.
Számoljuk egy ugrás diszkontinuitás mint a különbség a jobb és bal határok:
azaz ütemezés lemegy 4 db.
Aszimptota ott. Kétféle első diszkontinuitás az x = -2 egy ugrás egyenlő 5, és x = 2, egy ugrás egyenlő -4.
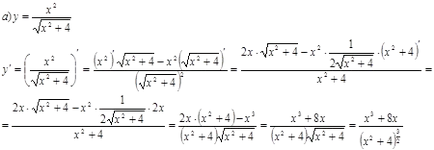
Keresse meg a származékai ezeket a funkciókat.
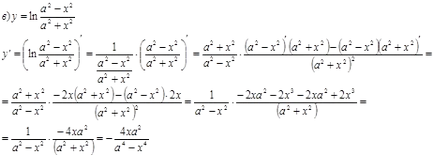
Keresse meg a bázis sugara és magassága a legkisebb térfogatú kúp körülírt körülbelül R sugarú labda
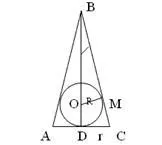
Ábra tengelyirányú metszete a kúp.
ABC - egyenlő szárú háromszög AB = BC;
Mintegy - a központ a beírt kör;
M - az érintkezési pont a kerülete a BC oldal;
D - érintési pont a háromszög alapja okuzhnostyu.
Legyen a kúp magassága egyenlő x, majd a háromszög OBM (négyszögletes)
Háromszögek VSD és TLT hasonló a két sarkában, akkor az egyenlőség:
Találunk a kötet egy kúp:
Megvizsgáljuk a függvény V (x) a szélsőérték:
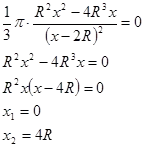
Azt látjuk, hogy egy pont x = 4R minimum pontot. Következésképpen, a legkisebb térfogata a kúp magassága h = 4R
Sugara a legkisebb térfogatú kúp:
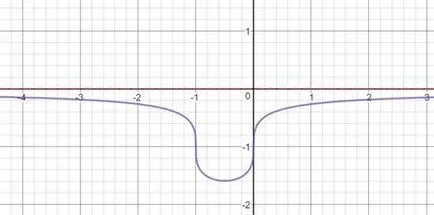
Fedezze módszerek differenciálszámítás függvények és telek:
1) meghatározzuk FIELD
2) paritás, páratlan.
Mi ellenőrzést végzünk, hogy bármelyik egyenlet:
Ebben az esetben a függvény lesz még
Ebben az esetben a függvény lesz furcsa
Ezért ezt a funkciót sem, még nem is furcsa. az általános formája a funkciót.
Arra a következtetésre jutottunk, hogy a grafikont a funkció nem szimmetrikus bármely tengely Oy. sem a származás.
Ez a funkció nem periodikus.
4) Folytonosság funkciót.
Az egész tartomány e függvény folytonos egy többtagú.
5) A metszéspontok a tengelyek
A metszéspontok ökör
Ez a függvény a diagram nem metszi a tengelyt Ox.
A metszéspontok az Y tengellyel
Így a metszéspont pontban (0, -1)
6) funkció módon végződik tartományban.
A végén a mező definíció szerint „- # 63,” és a „+”. Találunk a korlátokat a funkció
Ez jelzi a jelenlétét egy vízszintes asymptote y = 0.
5) A kritikus pontok a funkció, az időközönként monotonitás
Ahhoz, hogy megtalálja szélsőértékében a funkciót, akkor megtalálja a származékos és állítsa nullára, a gyökerei ebben az egyenletben a kritikus pontokat.
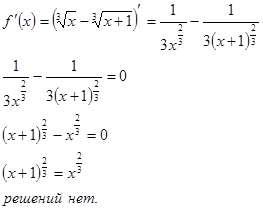
Nem szélsőérték pont.
6) inflexiós pontok, intervallumok konvexitás, konkáv
Találunk az inflexiós pont. Ehhez meg kell találni a második függvény deriváltját és azonosítja azt a nullához. A gyökerek a kapott egyenlet lesz az inflexiós pont a megadott függvény grafikonját.
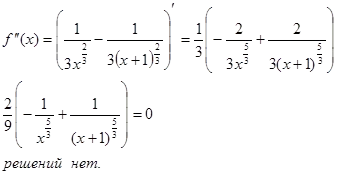
Nem inflexiós pont.
7) Ábrázolja a