Laboratóriumi munka №10 tanulmány a jog normális eloszlás a mechanikai modell
1. megtekintéséhez normális (Gauss), és a Maxwell eloszlás valószínűségi változók.
2. Olvassa el a normális eloszlás a mechanikai modellt, és meghatározzák annak varianciája, és mérjük a pontosságot.
elméleti bevezetés
Véletlen események által leírt elmélet a valószínűség, és előzetes statisztikai törvényeket, lehetővé teszi számunkra, hogy megtalálják a valószínűsége egy esemény egy sor véletlenszerű események, az átlagos érték egy véletlen változó, a legvalószínűbb eltérést az átlagtól, stb Mindezek a jellemzők határozzák meg egy véletlen változó eloszlása jog - azaz a függőség az előfordulási valószínűsége egy adott érték egy véletlen változó értékének értékét.
Nézzük - diszkrét valószínűségi változó, értékeket vehet fel s: x1. x2. ... xn. ... xs. Ezek az értékek megfelelnek a valószínűségek: p1, p2. ... Pm. ... ps. Például Pm annak a valószínűsége, hogy a szóban forgó mennyiség kerül az értéket Xm. Az összeg minden valószínűség (P1 + P2 + ... + ps) annak a valószínűsége, hogy a vizsgált fogják értékesíteni bármilyen (nem számít, hogy milyen) a értékei x1. x2. ..., xs. Ez a valószínűség egyenlő eggyel.
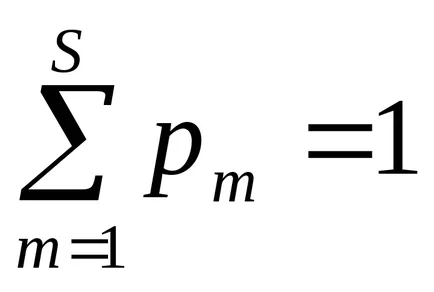
P1 valószínűsége. p2. ... ps körű információkat tartalmaz a véletlen változó.
Azonban sok esetben, a gyakorlatban a tudás valószínűség nem szükséges. A két legfontosabb jellemzője a valószínűségi változó ahhoz, hogy tudja - annak átlag és szórás.
Az elvárás az átlagos értéke a véletlen változó. Átlagoltak nagyszámú vizsgálatok. Utal nak az ilyen közepes fogja használni kacsacsőrök
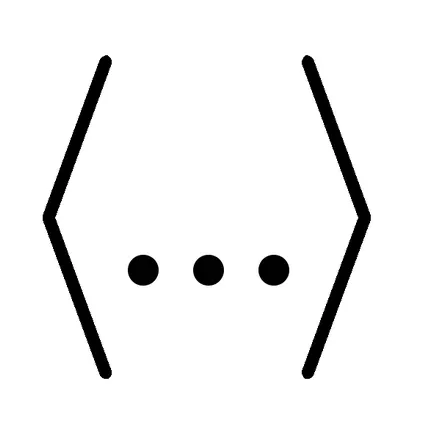
Az átlagos értéke a valószínűségi változó összege termékek értékei valószínűségi értékek felelnek meg:
vagy használja a jele összegzés
Amellett, hogy az átlagos érték, az is fontos tudni, hogy mennyi az értéke a mennyiség eltér az átlagos érték, vagy más szóval, hogy milyen széles körben elterjedt a véletlen változó.
Az átlagos értéke átlagos eltérés (az átlagos különbség értéke
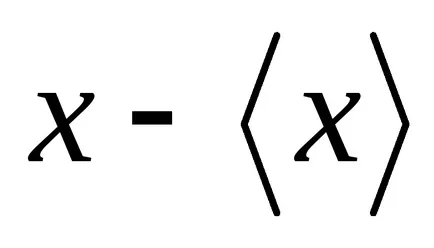
.
Ezért figyelembe véve az átlagos érték nem eltérések az átlagtól, és a tér az eltérés, azaz:
Ez a szórás a véletlen változó. amely jelöljük
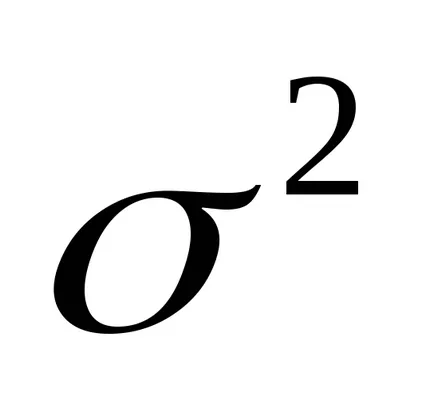
Négyzetgyöke a szórás
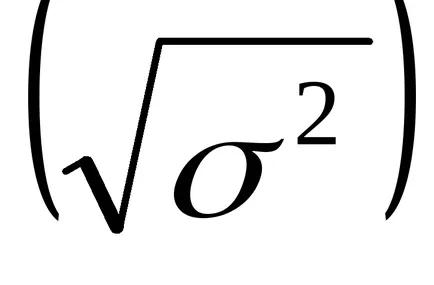
Így a valószínűségi változó jellemzők - a várható értéke és szórása - diszkrét változók által kifejezett összege a valószínűségi eloszlása (a (2) képletű - (4)).
Folyamatos véletlen változók helyett az alkalmazott mennyiségben integrálok, hanem a valószínűségi eloszlás valószínűségi eloszlást:
ahol f (x) - a valószínűsége sűrűsége a valószínűségi változó.
Hadd magyarázzuk, hogy mit jelent a valószínűség-sűrűség. Legyen egy sor nagyszámú N értékek valószínűségi változó. Példa - egy sor N mérésekhez eredmények egy fizikai mennyiség, amely lehetővé teszi a meghatározását véletlen hibák. Példa a molekuláris fizika - egy sor nyúlvány értékek bármilyen tengely a gáz sebességét részecskék. Hagyja, hogy a véletlen változó dN értékek közötti tartományban x-x + dx. A nagysága dN arányos a szélessége dx nyílás száma N. and Law (funkció) vagy valószínűségi sűrűség eloszlását a valószínűségi változó függvénye:
Kifejtse a fizikai jelentése az eloszlási függvény meghatározott dx = 1, azaz figyelembe vesszük az egység intervallum az értékek a véletlen X változó x + 1. Ebben a képletben (7) egyszerűsített és formáját ölti:
Következésképpen, az eloszlásfüggvény azt mutatja, hogy milyen arányban a teljes számának értékei a valószínűségi változó egységnyi tartományban x és x + 1.
Más szóval, az eloszlásfüggvény jelzi annak a valószínűségét, hogy a véletlen változó vett véletlen érték beleesik az egység intervallum x x + 1.
Sok esetben a leírás valószínűségi változók csak az úgynevezett normális eloszlás (Gauss eloszlás). Ez az eloszlás akkor jelentkezik, ha a véletlen érték számos tényezőtől függ, amelyek hozzájárulhatnak egyenlő valószínűséggel pozitív és negatív eltéréseket. Ennek egyik példája a eloszlása véletlenszerű hibák a mérési bármilyen fizikai mérete vagy a megoszlása a nyúlványok a koordináta-tengely irányában a gáz részecskesebesség. Meg lehet mutatni, hogy a törvény a normális eloszlás (Gauss-törvény) a formája:
ahol x - tetszőleges értéket a valószínűségi változó;
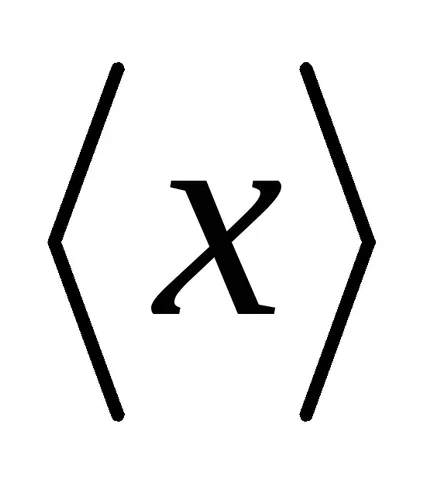
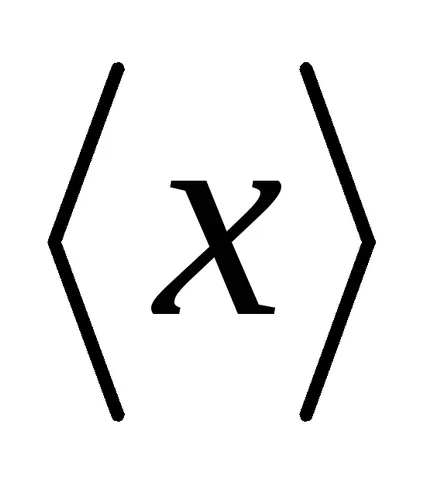

1. ábra - ütemezése Gauss-féle eloszlás.
1 -
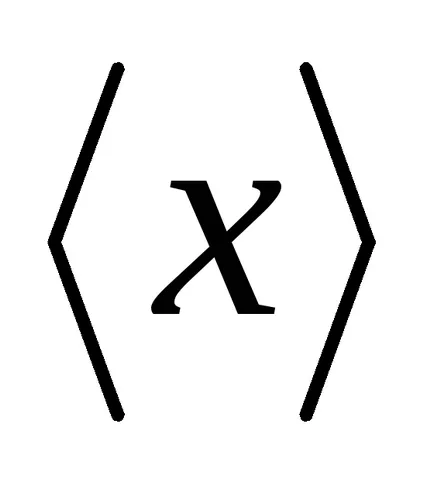
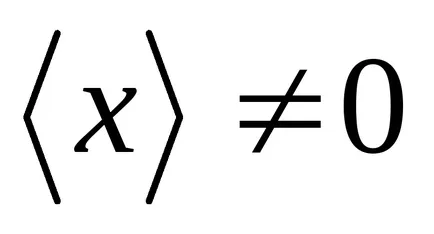
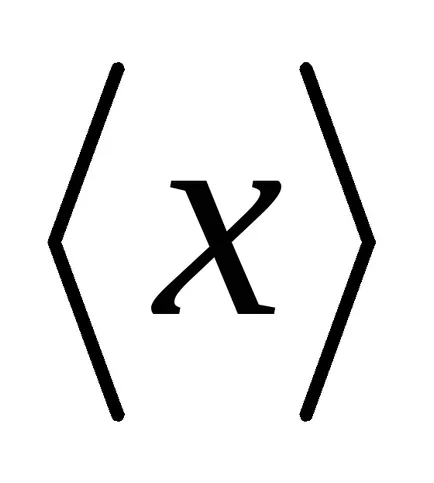
A normális eloszlás jellemzi, hogy olyan intézkedés pontosság
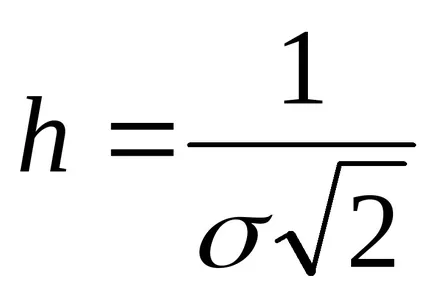
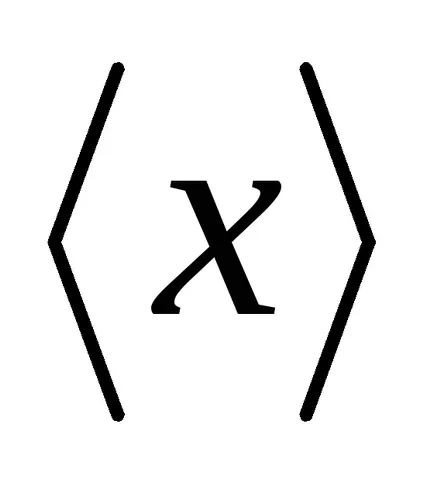
.
érték
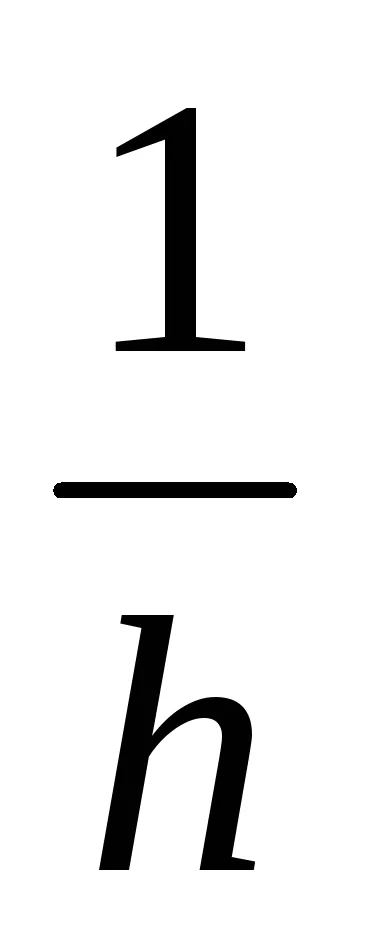
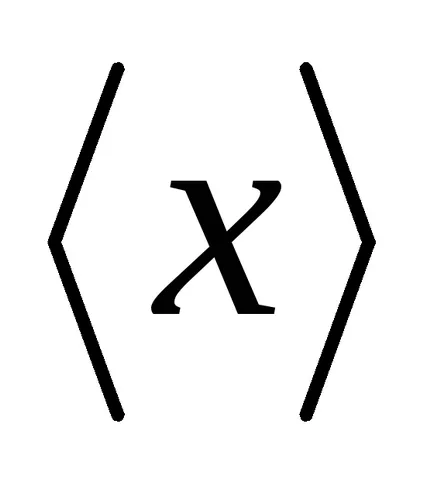
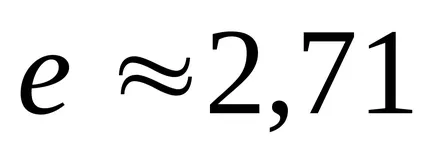
Így, a normális eloszlás írja le a valószínűsége sűrűsége folytonos valószínűségi változók, a változása értékek, amely által okozott különböző tényezők ható megközelítőleg egyformán és egymástól függetlenül. A maximális az eloszlás (1. ábra) elérésekor egy x értékét. egyenlő elvárás
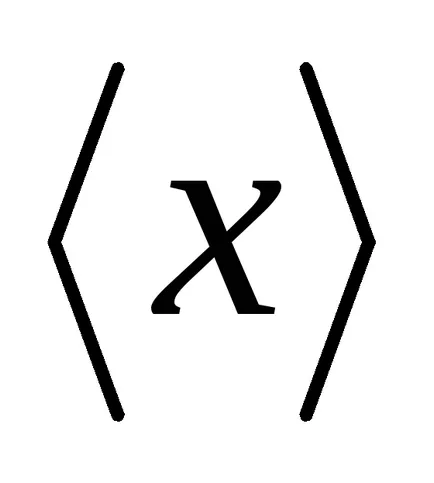
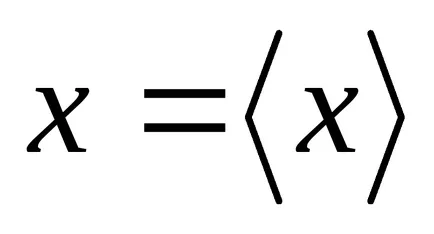
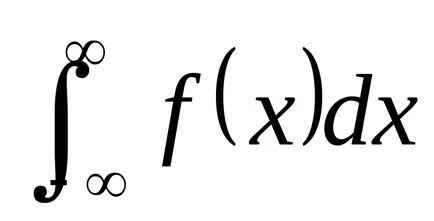
Elosztjuk az alatti terület Gauss-görbe (2. ábra) a függőleges vonalak a egyedi adagokban. Először is, úgy a része, amely megfelel a rés.
Láthatjuk, hogy
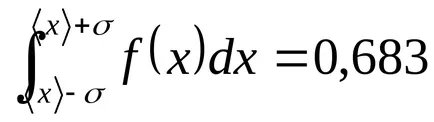
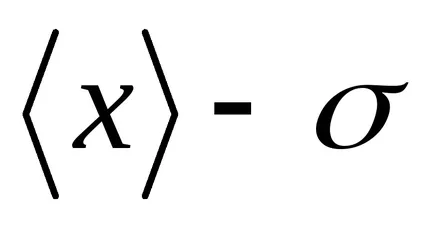
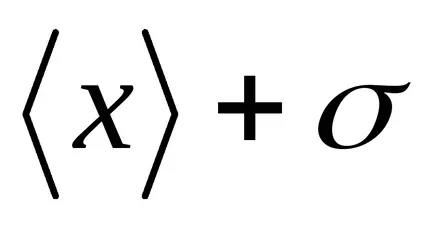
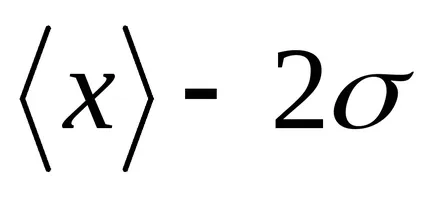
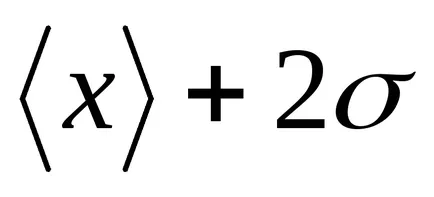
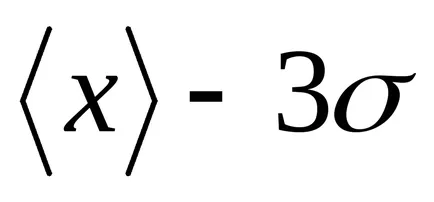
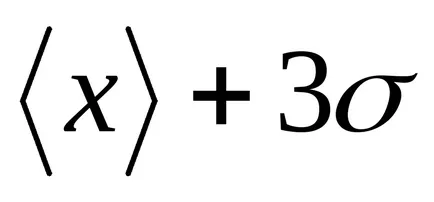
T

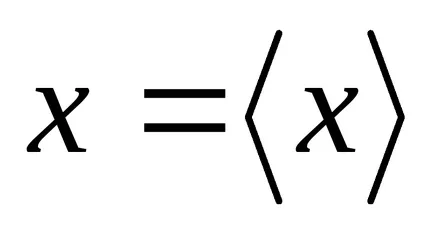
Risunok2 - A szabály „három szigma”
Amint a fentiekben említettük, a vetítési részecskesebesség VX gáz x-tengely a valószínűségi változó a Gauss-féle eloszlás törvény, fogadó ebben az esetben a forma:
ahol m - részecske tömege; k - a Boltzmann állandó; T - abszolút hőmérséklet. Az összehasonlításból (9) és (10) következik, hogy az átlagos sebesség a nyúlvány
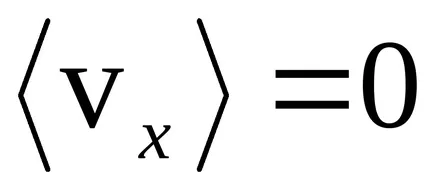
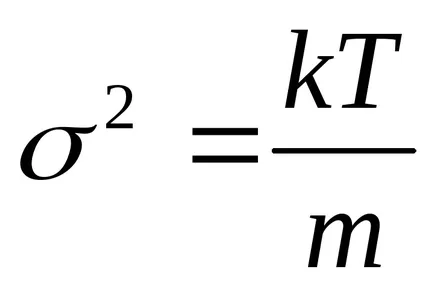
Ezzel szemben a sebesség kiemelkedést befogadó mind negatív, mind pozitív értékek, a számérték (modulus) az részecskesebesség nem lehet negatív. részecskesebesség gázmodul - szintén egy véletlen változó, de nem írja le egy Gauss-féle, de az úgynevezett maxwelli gáz részecskék eloszlásfüggvény skorostyamF (V), társított Gauss-féle eloszlás nyúlványok képletű sebesség:
A grafikon a F (v) (3. ábra) azt mutatja, hogy a legtöbb gáz részecskesebesség közel van az úgynevezett legvalószínűbb sebesség VB. A részecskék aránya, amelyek egy nagyon kis (v → 0), vagy nagyon nagy sebességgel (v → ∞), kicsi.
