Lineáris elválaszthatatlan és forgalomba vektormez®
Meghatározása lineáris integrál
Tegyük fel, hogy a térbeli tartomány $ \ mathbf> $ folytonos vektor mező $ \ bar (\ mathbf>) \ mathbf> $ - sima görbe fekvő $ \ mathbf> $. A vonalintegrál a mező $ \ bar $ vonal mentén $ \ mathbf> $ nevezzük vonalintegrál hossza mentén az ív a belső termék $ \ bar (\ mathbf>) $ a készüléken érintő vektor $ \ bar (\ mathbf>): W = \ int \ limits_L (M) \, ds> $.
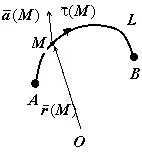
A fizikai jelentése lineáris integrál.
Ha $ \ bar (\ mathbf>) $ - erőtér, a $ W $ az a terület, ezen a ponton halad az anyag egy vonal mentén $ \ mathbf> $ lásd hármas integrálok ..
Az alapvető tulajdonságok lineáris integrál.
$ \ Int \ határok _ \, ds> = \ int \ határok _ \, ds> + \ int \ határok _ \, ds> $. Irány az egyes részeinek a $ \ mathbf> _ $ és $ \ mathbf> _ $ azonosnak kell lennie, mint az egész görbe $ L_1 \ cup L_2 $,
3). Amikor az irányba $ \ mathbf> $ lineáris szerves előjelet.
Ez abból következik, hogy a vektor $ \ bar (\ mathbf>) $ változik - $ \ bar (\ mathbf>) $.
4). Ha $ \ mathbf> $ - vektor mező vonal és irányában mozdul el a területen, akkor a $ \ mathbf >> 0 $. Ebben az esetben a vektor $ \ bar (\ mathbf>) $ egyenesre $ \ bar (\ mathbf>) $, így $ \ bar \ cdot \ bar = \ mathop \ bar> \ limits_> = \ vert \ bar \ vert> 0 $.
Kiszámítása a vonalintegrál
Mint minden vonalintegrál, vonalintegrál számítjuk redukcióval határozott integrál a paraméteres görbe tipikusan számítjuk vonalintegrál $ W = \ int \ limits_L $. Ha a görbe parametrikus specifikáció az űrlap $ L: \ left \integrálása a mozgás iránya által meghatározott irányt a görbe.
Forgalomban vektormez®
Forgalomban az úgynevezett vonalintegrál vektor mező egy zárt görbe $ \ mathbf> $: U $ = \ OINT \ limits_C> $.
Ez általában azt mondta, hogy a keringés jellemzi a forgási kapacitása terén. Ez arra utal, hogy a következő. Ha a vektor erővonalak zárva vannak, akkor, mint láttuk, a forgalomban ez a tér irányában pozitív, míg a hidrodinamikus értelmezése részecskék szálképző folyadék ezekre zárt vonalak. Tegyük most fel, hogy a jelenlegi vonalak önkényes, elképzelni az összeg $ \ mathbf> $ a zárt szelvényű $ \ mathbf> $. Ha ennek eredményeként a mozgást, ez az áramkör fog forogni a mező forgási kapacitása, az abszolút értéke a forgalomban fogja meghatározni a szögsebesség U $ \ vert $, annál nagyobb a sebesség>, keringési jel jelzi, hogy a forgásirány egybeesik az integráció irányába.
Lásd még:
Mechanikus vonatkozó kettős integrál
A számítás a felületi integrál az első fajta
Tulajdonságok kettős integrálok
Formula. Egyenlőség funkciók és átszámítási képleteket. Key egyenértékűség
Ide tartalmát $ \ Rightarrow \ Rightarrow \ Rightarrow $