Meghatározása az átviteli függvény a rendszer által képviselt tömbvázlata
Meghatározása az átviteli függvény a rendszer, a tömbvázlata, amely az 1. ábrán látható
1. ábra - A blokkdiagramja SU
Vegyület blokkolja a transzfer függvény és olyan vegyület, negatív visszacsatolás.
Átviteli függvénye ezen egységek fogja meghatározni a következő képlettel
Blokkok átviteli függvények és olyan vegyület pozitív visszacsatolás.
Átviteli függvénye ezen egységek fogja meghatározni a következő képlettel
Az átviteli függvény a teljes rendszer fogja meghatározni, amelyet a képlet
Ha ebben az esetben a számértékek az átviteli függvény a rendszer formájában fog
Meghatározó típusú kapcsolatok
1) Link az átviteli függvény - aperiodikus link.
Az általános nézet az átviteli függvény
ahol - az erősítés a link;
Egy adott szintű együtthatók
2) Link az átviteli függvény - aperiodikus link.
Az általános nézet az átviteli függvény
ahol - az erősítés a link;
Egy adott szintű együtthatók
3) Link az átviteli függvény - pillanatnyi teljesítmény.
Az általános nézet az átviteli függvény
ahol - az erősítés a link;
Egy adott szint aránya
Meghatározása egy differenciálegyenlet, amely leírja a rendszer
Okonchalno differenciálegyenlet válik
Meghatározása az átviteli függvény a rendszer, a tömbvázlata, amely a 2. ábrán látható
Az átviteli függvény a blokk.
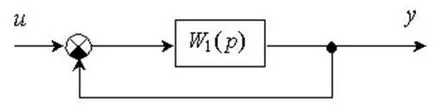
2. ábra - A blokkvázlata a vezérlőrendszer
Átviteli függvénye a rendszer határozza meg a képlet
A karakterisztikus polinomja a rendszer formájában
Annak megállapításához, az egyenlet rendszert megoldott oszlopok (lásd a határozat. Függelék)
Hely adatainak pólusok a komplex síkban van a 3. ábrán látható.
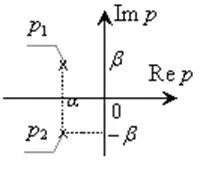
3. ábra - Hely a komplex-konjugátum rendszer pólusai
Meghatározása a rendszer időzítése
A tranziens válasz a kép határozza meg:
ahol - az átviteli függvény a rendszer.
Ezután a rendszer irányításának
Eredeti tranziens válasz határozza meg a képlet
ahol - a levonás az integrandus, - pólusai az integrandus.
Így a maradékokat határozzuk:
A tranziens válasz az eredeti megjelenés
A grafikon a tranziens válasz a 4. ábrán látható
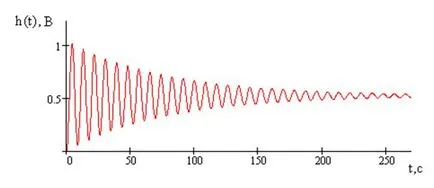
4. ábra - diagramja tranziens válasz
A impulzusválasz számítjuk differenciálásával tranziens válasz
akkor a impulzusválasz a formája
A grafikon az impulzus válasz az 5. ábrán látható.
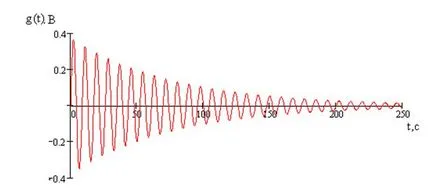
5. ábra - Graph az impulzusválasz
Meghatározása a fő mutatók minőségének az átmeneti folyamat tranziens
Az ütemterv szerint határozza meg a tranziens válasz a közvetlen mutatók a minőség.
1) túllövés σ - értékének első kibocsátási relatív tranziens válasz, azaz.
2) a tranziens tn - az időt, ami után az output folyamat nem megy túl a határain területén
3) a statikus hiba - hiba az állandósult állapotban a kereset az álló jelzőrendszer.
ahol - a bemeneti jel,
- Állítsa be az értéket az átmeneti folyamat.
Annak megállapításához, a frekvencia karakterisztika, és hogy egy ellenőrzési rendszer (frekvenciamenete, fázis válasz, LACHH, LFCHH, ALACHH)
Az átviteli függvény az ellenőrzési rendszer formájában
Komplex transzfer koefficiens az űrlap
Alapján a kapott expressziós, frekvencia és fázis válasz a rendszer lesz:
Frekvencia és fázis válasz grafikonok ábrán mutatjuk be a 6. és 7. ábrákon
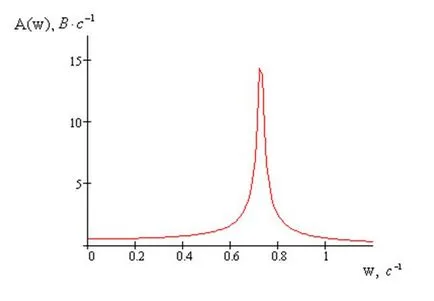
7. ábra - Graph AFC
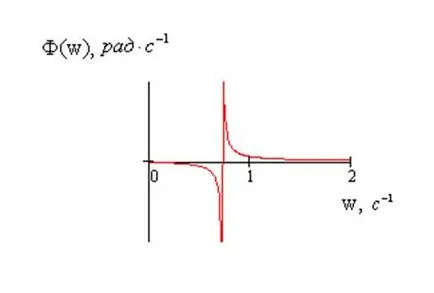
8. ábra - Schedule PFC
ha ábrázoljuk az x tengelyen.
LACHH grafikon a 9. ábrán.
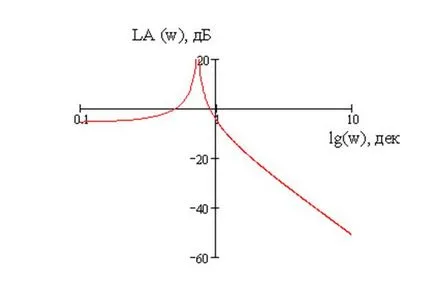
9. ábra - Graph LACHH
Építőipari logaritmikus aszimptotikus frekvenciamenet (ALACHH).
Ehhez nyújt átviteli függvénye egy tipikus kapcsolat
Az átviteli függvénye egy zárt hurkú rendszer a következő:
majd transzformált transzfer függvény a forma:
A rendszer egy rezgő elem.
A nyereség az egység.
Gyakoriságának meghatározásakor a töréspontot. Ahhoz, hogy ezt, meg az értékét állandó szinten az idő:
Ezután a frekvencia kitörési pont:
Meghatározása metszéspontjait az alacsony frekvenciájú aszimptotákkal keresztül erősítési szint
A rezgő egység meredekség - 40 dB / dekád.
ALACHH grafikon a 10. ábrán látható.
meghatározása sávszélesség
A sávszélességet meghatározó a 11. ábrán látható

11. ábra - meghatározása sávszélesség
Elemzés a rendszer stabilitását. Meghatározása a biztonsági tényező.
1. A root módszer
A rendszer a következő oszlopok:
Hely adatainak pólusok a komplex síkban van a 11. ábrán látható.

12. ábra - Hely a komplex-konjugátum rendszer pólusai
Következésképpen, a rendszer aszimptotikusan stabil, mert azzal a feltétellel
vagyis a valós része a gyökerek nullánál kisebb.
2. Az eljárás Routh-Hurwitz
Karakterisztikus egyenletének formájában
Hurwitz mátrixot együtthatók az egyenlet
Ezért, a rendszer stabil.
3. Mihajlov stabilitási kritérium
A karakterisztikus polinomja a vezérlő rendszer a következő:
Jellemző komplex keletkezik helyett az érv tisztán képzetes változó:
A valós és képzetes része:
Hodográfot kapunk Mikhailova a 13. ábrán látható.
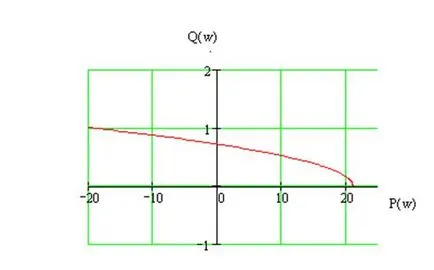
13. ábra - hodográfot kapunk Mikhailova