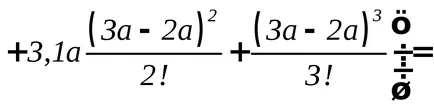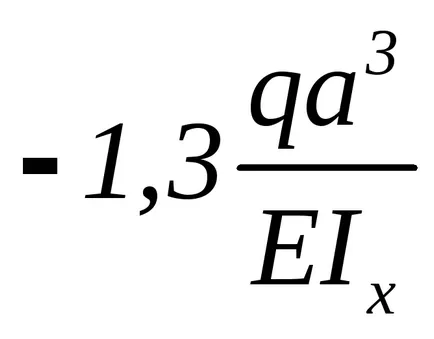Meghatározása deformáció a gerenda hajlítási
Deformációja gerendák hajlítási. A differenciálegyenlet egy íves nyaláb tengelye. A módszer a kiindulási paraméterek. Univerzális egyenlet a rugalmas vonalat.
6. deformációja gerendák alatt sík hajlító
6.1. Alapfogalmak és meghatározások
P
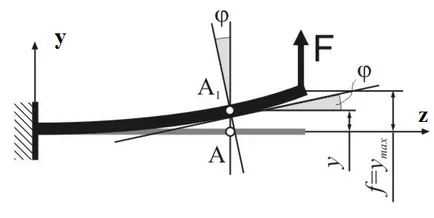
Deformációja gerendák hajlítási leírjuk két paramétert:
lehajlás (y) - elmozdulása a súlypont a nyaláb keresztmetszetében merőleges irányban
Ábra. 6.1 tengelyére.
Nem tévesztendő össze az eltérítési y y koordináta pontok a gerenda rész!
Maximális elhajlása a gerenda nevezzük SAG (F = ymax);
2) forgását a szekció szög () - szög, amelyben a keresztmetszet képest elfordul az eredeti helyzetébe (vagy közötti szög az érintő a rugalmas vonalat és az eredeti nyaláb tengelye).
Általában a sugáreltérítési értéke egy adott pont egy koordináták függvényeként és z felírható a következő egyenlet:
Ezután közötti szög az érintő a görbe a fénysugár tengelye és az X tengely határozza a következő kifejezésből:
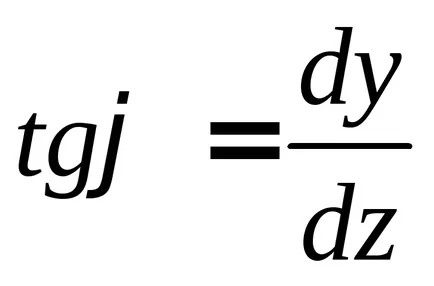
Tekintettel a kicsinysége miatt a szögek és elmozdulások, akkor feltételezhetjük, hogy
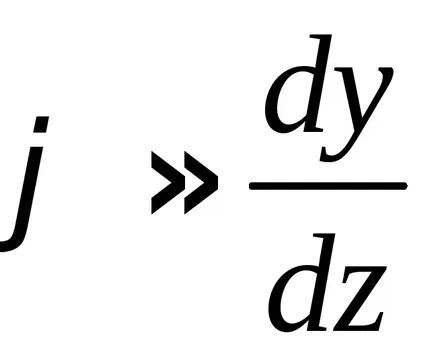
a forgásszög a rész az első deriváltját a lehajlás a gerenda az abszcisszán szakaszt.
6.2. A differenciálegyenlet görbült nyaláb tengelye
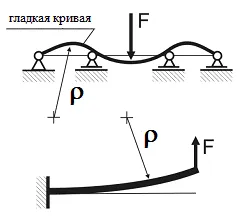
Ennek alapján a fizikai természetét hajlító jelenség azt mondhatjuk, hogy a folyamatos ívelt az optikai tengely folyamatosnak kell lennie és sima (melyeknek nincs törés) görbét. A deformáció egy részének a sugár határozza meg a görbület a rugalmassági görbe, azaz görbület a nyaláb tengelye.
Korábban képlet meghatározására a görbület a faanyag (1 / ρ) kapunk, a hajlító
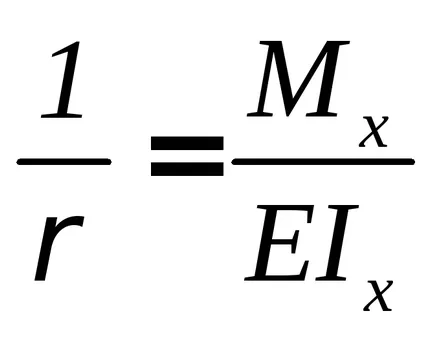
Másrészt, természetesen magasabb matematika Ismeretes, hogy az a sík egyenletét görbületének görbe a következő:
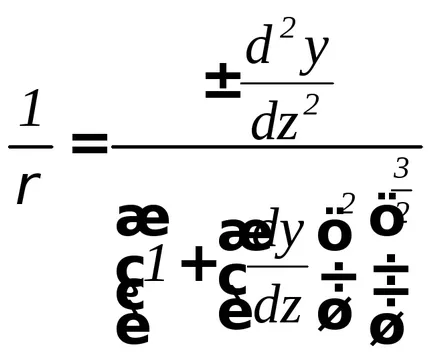
Egyenlővé a jobb oldalán ezen kifejezések, megkapjuk a differenciálegyenlet a hajlított a fénysugár tengelye, az úgynevezett pontos egyenletet ívelt nyaláb tengelye
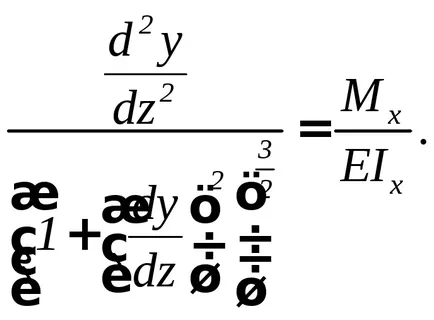
A koordináta-rendszer teknők z0y. Ha az Y tengelyen pedig felfelé, a jel határozza meg a jel az idő a második származékot y és z.
Az integráció ebben az egyenletben nyilvánvalóan nehézséget okozhat. Ezért általában írva egyszerűsített formában, figyelmen kívül hagyva az érték a zárójelben képest egységét.
Ezután a differenciálegyenlet a rugalmas vonal a gerenda figyelembe kell venni a formában:
A megoldás a differenciálegyenlet (6.1), azt találjuk, integrálásával mindkét oldalán több mint a variábilis z:
Az integrációs állandók C1. D1 megtalálható a peremfeltételek - feltételek gerenda rögzítő, a gerendák fogja meghatározni az állandó az egyes területekre.
Tekintsük adatokat eljárás egy konkrét példát egyenletek.
A konzolos rúd L hosszúsága. betöltve egy keresztirányú erő F. anyagsugár (E), az alakja és mérete a szakasz (Ix) is feltételezzük, hogy ismert.
Oh
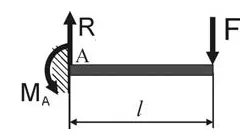
a) meghatározzák reakciót zadelke
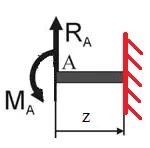
c) meghatározza az elfordulási szög a gerenda szakaszok
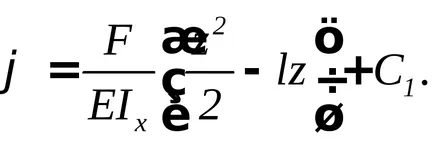
A konstans C1 található a rögzítési feltételeket, nevezetesen - egy tömített az elforgatás szöge nulla, akkor
Azt találjuk, a forgásszög a szabad végén a fény (Z = l):
A „mínusz” jel azt jelzi, hogy a szakasz óramutató járásával megegyező irányba.
d) meghatározza a sugáreltérítési:
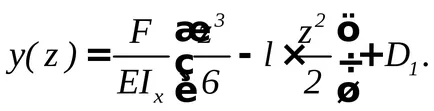
Állandó D1 megtalálható a rögzítési feltételeket, nevezetesen - egy tömített a lehajlás nulla, akkor
Azt találjuk, a lehajlás a szabad végén a fény (X = l)
.
A „mínusz” jel azt jelzi, hogy a keresztmetszet leesett.
6.3. Univerzális egyenlet a rugalmas vonalat. Módszer kezdeti paraméterek
A leírt technika meghatározására az elmozdulás gerendák, amely több szakaszok, meglehetősen időigényes, mivel az n számú tetszőleges konstansok részek (C és D) növeli, mint 2n. Ahhoz, hogy csökkentsék a számítási munka ilyen esetekben, hogy kifejlesztett számos módszer, beleértve az eljárás kezdeti paraméterek, amely lehetővé teszi tetszőleges számú helyek, hogy csökkentsék a megoldást találni a csak két állandók - eltérítési és a forgatási szöget a származási.
D
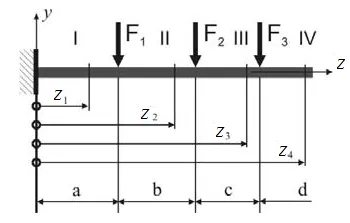
1) az eredete koordinátákat kell kiválasztani közös az összes oldalak a bal szélső pontja a gerenda;
2
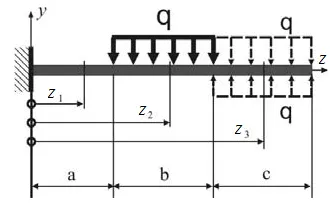
3) esetén elosztott terhelés szünetet ez kiterjed a végén a fény, és visszaállítani a tényleges terhelési feltételek beadott „kompenzáló” fordított terhelés
4) integrálása az egyenlet minden területen nem felfedve a zárójelben.
P
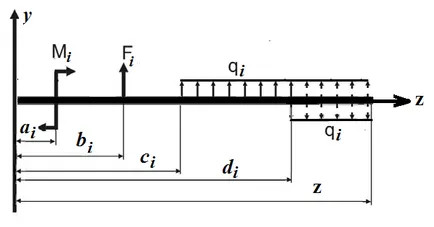
PostoyannyeDi (i = 1, 2, 3, 4, 5) úgy kell megválasztani, hogy a keresztmetszete a lehajlás függvény balkiypri átmenetet szakaszról szakaszra folyamatos. Amennyiben a következő feltételeket:
Alkalmazása a szuperpozíció elve, írunk az egyetemes egyenlet a hajlított tengelye legáltalánosabb formája:
Differenciálás (6.7) megkapjuk az egyenletet meghatározására az elfordulási szögek:
Meghatározási módszere az eltérítési és elforgatással a gerenda képletei alapján (6,7-6,8) nevezzük a módszer kezdeti paraméterek.
Megjegyezzük, hogy a problémák megoldását célszerű írni az egyenletet első univerzális legtávolabb van a származási hely, akkor az egyenlet az előző szakaszok könnyen, áthúzása a kapott kifejezéseket az egyenlet, figyelembe véve a terhelés a következő részekben.
Odnoprolotnaya gerenda konzol befolyása alatt elosztott nagruzkiq (ábra. 6.3). Find hajlító differenciálegyenlet, és megtalálja alakváltozása és az elfordulási szögek a fesztávközi gerendák és végén annak kar részét a kezdeti paramétereket.
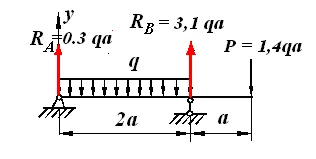
Alkotunk az egyenlet egyensúlyi:
Annak igazolására, hogy a talált választ érték a harmadik egyenlet - az összeg a nyúlványok a függőleges y-tengely:
Ezért a reakciót talált igaz.
Kiszámításához a deformáció a gerenda a megoszló terhelés univerzális egyenlet kell elérni a megfelelő végén a fény. Ezért elosztott terhelés-nek továbbra is a jelentési szakaszban, és hozzá az azonos, de ellentétes irányú (6.4 ábra). Hozzáadása az azonos terhelés következtében a törzs, amely statikusan nullával egyenlő, amely nem okoz változást a deformált állapotban a fény.
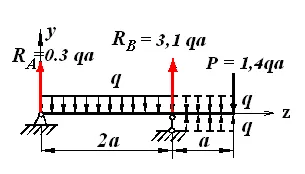
Írunk az egyetemes egyenlet:
On tartógerendák z = 0, z = 2a van y = 0.
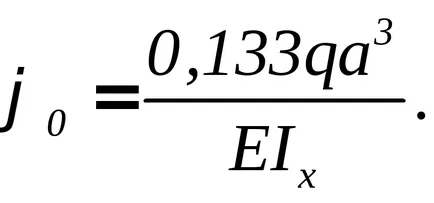
Így az egyetemes egyenlet:
Annak meghatározására, elforgatási szögek hossza mentén gerenda szakaszok különbséget ez az egyenlet:
Határozza meg a alakváltozása a közepén a gerenda span, és a végén a kar keresztmetszete.
;
Most határozzuk meg a forgásszögek részből áll: