Meghatározása koordinátáit több ponton Hansen feladat lineárisan szögálláshoz besorolás

feladat Hansen

A Hansen probléma a koordinátái két P és Q pontok az ismert koordinátáit a két A és B pontok, és a négy sarkát, mért meghatározott pontja (ris.2.15), hogy van, a probléma a Hansen kettős visszajelzést sarokban bevágás.

Kiindulási adatok: XA, YA, XB, YB.

Mért elemek: B1, B2, B3, B4.

Ismeretlen elem: XP, YP, XQ, YQ.

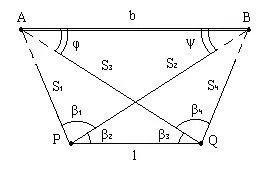
Grafikai megoldás. Mark két lap átlátszó papír (pausz) és épít szögek nekik: egy lapra - a szögek B1 és B2, a másik ajtólap - szög B3 és B4. Alkalmazza a rajz (terv vagy térkép) a két lap és a mozgó őket önkényes módon, hogy összekapcsolják irány szög a következő lapokat a pont, A és B a rajzban. Perekolot P és Q pontokat a rajzban.

Analitikus megoldása. Számos módja van, hogy megoldja a problémát, a Hansen; összefoglalja azokat.

Hogy oldja meg a problémát inverz között A és B pontok, vagyis kiszámítani a hosszát b az AB szakasz és azimut irányban BAB AB.

Adni egy tetszőleges egységnyi hossza megegyezik a hossza L PQ intervallum; L = 1,000.

Számítsuk szegmensek S'1 = AP, s'3 = AQ, S'2 = BP, S'4 = BQ tetszőleges egységekben segítségével egy első szinusz tétel háromszög PAQ, majd PBQ háromszög:

Számítsuk egységekben hossza b „a szegmens háromszög AB QAB a koszinusz:

és ellenőrzésére - az PAB háromszög:

Mindkét érték meg kell egyeznie.

Számoljuk a skálázási tényező k:

és összes számított távolságokat a valódi egység hossza:

Számítsuk ki a szög a fi QAB háromszög koszinusz:

Számítsuk ki a W szög a PAB háromszög számára koszinusz:

Számítsuk azimut irányba AQ:

és megoldani a problémát egy egyenes geodéziai pont pont Q:

Számítsuk ki a azimut irányát BP BBP BBA = - n, és a probléma megoldására egy egyenes geodéziai B pont, hogy a P pont:

Hely kiindulási pontok és a pontokat lehet meghatározni úgy, hogy a szegmensek PQ és AB metszik (2.16 ábra); megoldása során a probléma ugyanaz marad, csak megváltoztatni a kijelölését sarkait és oldalait. Továbbá, ha bebizonyosodik, hogy ebben a kiviteli alakban, a pozíciókat a P és Q pontok határozzák többször pontosabban, mint az általános kiviteli alak.

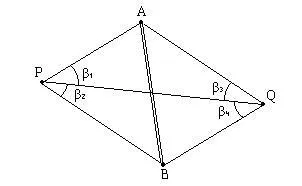
Az egységes probléma Hansen nincs ellenőrző méréseket, így a gyakorlatban a négy sarkából a mérések nem korlátozódnak, és elvégzik minden további mérést.

Lineáris-szögálláshoz

Osztályozása egyenes és sarkos mozog

Annak megállapításához, a koordinátáit több ponton is alkalmazni a különböző módszereket; A leggyakoribb ezek közül lineáris-szög stroke, a rendszer lineáris és szögletes mozog, háromszögelés, háromszögelés és mások. Lineárisan szögálláshoz képviseli a szekvenciát poláros talpas, ahol a mért vízszintes szögek és távolság a szomszédos pontok (ábra 2.17).

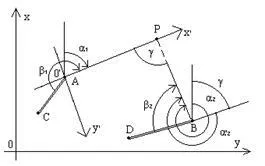
Kezdeti adatok alatt lineárisan szögkoordináták XA, YA pont, A és azimut BBA vonal BA, amely az úgynevezett kiindulási forrása irányszög; ez a szög lehet megadni implicit módon, a pont koordinátáit B.

Mért értékek - egy vízszintes szögek B1, B2. BK-1 és a BK távolságok S1, S2, Sk-1, Sk. Szintén ismert szög mérési hiba MW és relatív hiba távolságot mérő mS / S = 1 / T.

Irányított oldalán löket szögek szekvenciálisan számítva ismert képletek átviteli keresztül azimut elfordulási szög

A bal sarokban. (2,64)

A derékszög. (2,65)

Bekapcsolásához ábra 2.17 van:

Pontok koordinátáinak nyert megoldása során a közvetlen problémát geodezichekoy első pontból a 2. pont, majd a 2. ponttól a 3 pont, és így tovább kör végéig.

Lineárisan szögálláshoz, ábrán látható 2,17, nagyon ritkán használják, mivel hiányzik belőle a mérés vezérlő; A gyakorlatban, mint általában, alkalmazza az agyvérzés, amely ilyen ellenőrzés.

Alak és teljessége az eredeti adatok lineáris-szög stroke vannak osztva a következő típusok:

Nyitott pálya (2-18 ábra): a kiindulási pontok ismert koordinátájú és a kezdeti azimut ott az elején és végén a löket;

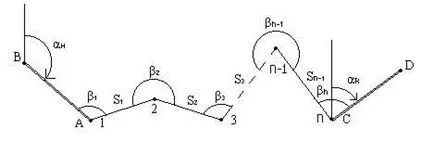
2.18. Vezetési nyitott zugú lineáris löket

Ha az elején vagy a végén a löket nem az eredeti azimut, akkor mozog részben rácsozott; Ha a forrás irányított szögek egyáltalán nem, akkor fut egy teljes rácsozott.

zárt lineáris-szögálláshoz (ris.2.19) - kezdő- és végpontját a stroke egyesítjük; egy pont stroke ismert koordinátái és az úgynevezett kiindulási pont; ezen a ponton kell a kiindulási vonal egy ismert irányszög, és a mért primychny közötti szög ebben az irányban, és az irányt a második bekezdésében a stroke.

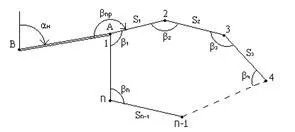
Ris.2.19. Reakcióvázlat zárt lineárisan szögálláshoz

Függő lineáris-szögálláshoz (ábra 2.17) van a kiindulási pont egy ismert helyen és a kezdeti azimut csak a folyamat elején a kanyar.

szabad lineáris-szög stroke nem a kiindulási pont és a kezdeti irányított szögek vagy az elején vagy végén a természetesen.

Szerint A mérés pontosságát a vízszintes szögek és távolságok lineáris-szög stroke vannak osztva két nagy csoportra: teodolittal mozog, és poligonometricheskih mozog.

A teodolit áthaladásánál vízszintes szögek mérjük egy hiba ne legyen nagyobb, mint 30”, a relatív hiba távolságot mérő mS / S tól 1/1000 1/3000.

A poligonometricheskih áthaladásánál vízszintes szögek mérjük egy hiba 0,4 „és 10”, és a relatív mérési hiba mS / S távolság a 1/5000 és 1/300 között változik 000 By mérési pontosság poligonometricheskih átjárók vannak osztva két bit és négy osztályba (lásd. Szakasz 7.1).