Meghatározó tehetetlenségi nyomatéka a henger és a relatív gördülő súrlódás, tartalom platform

Lab N 6

Meghatározó tehetetlenségi nyomatéka a henger

és az együttható gördülő súrlódás

Kísérleti meghatározása a tehetetlenségi nyomatéka a henger és egy gömb, összehasonlítva a tehetetlenségi nyomaték kísérletileg kapott és elméletileg.

2. Az elmélet a kérdés

A. A tehetetlenségi nyomaték az anyag pont határozza meg a termék a tömegét, és a tér a forgás sugara:

Különböző pontjain a valódi test különböző távolságokra a forgástengely, hogy minden tehetetlenségi nyomatéka tömegpontok -ról:

ahol dm - kicsi tömeget a szilárd test tagja.

Mivel a m = Rv, ahol r -. Matter sűrűségű, V - az a térfogat, a test, majd d m = r × dV, ahol dV - az a térfogat a testelem.

Ezután a (2) képlet formájában:

Példaként, úgy a kimenő nyomaték a homogén lemez a tehetetlenségi tengely síkjára merőleges a lemez és a középpontján átmenő (ábra. 1).

Osztjuk a lemezt gyűrű alakú dr réteg vastag. Minden pont egy réteg lesz azonos tengelyétől egyenlő r.

A kötet egy ilyen réteg:

DV = a × 2prdr, ahol - a lemez vastagsága.

Meghajtó homogén, r = const.

Szerint a (3) egyenletet kapjuk:

Végül, a lemez belépő m tömegű, egyenlő a sűrűség R a térfogata a lemezt p R2, kapjuk:

Ha a tengely (0 ¢ ¢ 0) merőleges a lemezre, hanem áthalad az éle (ábra. 1), a tehetetlenségi nyomaték határozza segítségével Steiner-tétel. Steiner-tétel van formuláivá a következőképpen: a tehetetlenségi nyomaték J képest egy tetszőleges tengely az összege a tehetetlenségi nyomaték párhuzamos tengely ez a test, és áthalad a tömegközéppont és a testtömeg termék m távolság négyzetének d tengelyek közötti:

Így, mint, és a d = R, akkor (7)

Mi ebből a homogén gömb tehetetlenségi nyomatéka körülbelül egy átmenő tengely közepén. Annak megállapításához, a tehetetlenségi nyomatéka a labda képest a központi tengellyel O osszuk a több elemi lemezek (DH vastag) XOU párhuzamos síkban (ábra. 2).

d h = r d J = Rcos j d j, ahol r = Rcosj

elemi lemez tömege r sugara egyenlő:

A tehetetlenségi nyomaték elemi lemez sugara r dm és a földi tengelyéhez képest O egyenlő:

Tehetetlenségi nyomaték, tengelyhez képest O kapjunk, összegzésével tehetetlenségi nyomatéka az elemi lemezek és halad, hogy korlátozzák az O (a féltekén).

Egy gömb tehetetlenségi nyomaték

Ezután a kötet egy gömb

(12) egyenlet meghatározza a tehetetlenségi nyomatéka a labda (gömb), mivel ez forog körül a tömegközéppont. Ha a labdát tengely körül forog, hogy nem halad át a súlypont, a tehetetlenségi nyomaték határozza Steiner-tétel (5).

B. A kinetikus energia egy test körül forgó rögzített tengely szögletes skorostyuw egyenlő

Ha a test forog, szintén halad előre, (sík mozgás), a mozgási energia összegével egyenlő a mozgási energia a transzlációs és rotációs mozgások:

Meghatározása tehetetlenségi nyomaték a labda készül ebben a munkában az idő függvényében a labdát gördülő egy ferde sík (3.).

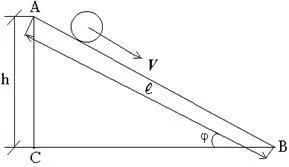
A tetején a ferde sík kinetikus energiája a labda nullával egyenlő, a potenciális energia mgh. A legalacsonyabb pont (B) a ferde sík a potenciális energiája a labda nullával egyenlő, a kinetikus energia

Ezen kívül, részben az energia megy dolgozni erőivel szemben súrlódás

A = m mg l cosj (15)

ahol m - súrlódási együttható, l - hossza a ferde sík, J - szög alatt az alapja a ferde sík. T. k., Ez a szög kicsi, akkor egy hiba nem haladja meg az 5% lehet tekinteni cosj = I, akkor

A törvény szerint az energiamegmaradás

Hiányában a csúszás szögsebesség kapcsolódó lineáris kapcsolatban: w =, ahol R - az elforgatás sugarának (a gömb sugara, henger).

W behelyettesítve (17), és csökken m, kapjuk:

Mi kifejezetten a sebesség a végén a ferde sík révén t időpontban, és a hossza L:

Képletű (18) formájában:

Ennélfogva, a tehetetlenségi nyomatéka egyenlő:

Képletű (20) kiszámítjuk a tehetetlenségi nyomatéka a henger és egy gömb.

B. gördülő súrlódás

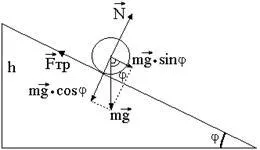
Henger (golyó) legördül a ferde sík az intézkedés alapján a három erő: a súrlódási erők és a megdöntött sík a reakció (4. ábra). A reakció szerint Newton harmadik egyenlő az abszolút értéke a normális komponense erő. amelynek nagysága mg × Sinj.

A súrlódás a henger és a ferde felület jön létre az érintkezési pontokon. Mivel ezek a henger pontokat minden időpontban vannak rögzítve (ezek képezik a pillanatnyi forgástengely), a súrlódási erő a súrlódási erő (görgő) nyugalmi. Csúszó gördülési a henger sík mentén, hogy hiányzik, feltéve, hogy a lineáris sebessége az érintkezési pontok nullával egyenlő, ami viszont akkor történik, ha a súlypont sebesség minden egyes alkalommal, amikor a szögsebesség w forgási a henger szorozva a sugár henger R

illetve gyorsulás ar központjában tehetetlenségi egyenlő a szöggyorsulással szorozva a sugár:

Ilyen körülmények között a súrlódási erő Tp nem haladja meg a maximális értéket és egy henger gördül majd csúszás nélkül.

Írunk a II-ik Newton-féle törvény gördülő henger (tál) a ferde sík:

Súrlódási nyomatékot tekintetében, a henger tengelyére nullától eltérő és egyenlő. Aztán alapján a II-nd törvénye dinamika a forgómozgást egy merev test felírható:

ahol J - tehetetlenségi nyomatéka a henger viszonyított forgástengelye egyenlő.

Megoldása egyenlettel 21, 22, 23, azt találjuk, hogy

Köztudott, hogy egy tapasztalt törvénye gördülő súrlódás:

ahol N - az erő a normál nyomáson, egyenlő a mi esetünkben mgcosj,

R - a sugara a henger, M0 - gördülő súrlódási együttható.

Egyenlővé jobb oldalán egyenletek (24) és (25) kapjuk:

Képletű (26) számítjuk a henger.

A labdát gördülő súrlódási együttható kapni függetlenül

3. A telepítés és mérési módszer

A telepítés egy ferde sík egy csúszda, amelyen a labda mozog. A tetején a labdát (henger) birtokában van egy elektromágnes, a legalacsonyabb pontja a vályú végálláskapcsolóval, hogy kikapcsolja az időzítőt. A stopper tartalmazza U = 220V hálózati, együtt egy elektromágnes relé a hálózatban - 24 V.

Attól függően, hogy a magassága a ferde sík változik a súrlódási együttható, ami által meghatározott képletek (26) és (27).

1. Állítsa rámpa legfeljebb £ h 15 cm, magassága mérésére h.

2. Tartalmazza a kimeneti csatlakozó stopperóra és egy elektromágnes.

3. Állítsa a tárcsát a „mágnes”.

4. Állítsa be a labdát (henger), a tetején az ereszcsatorna.

5. Kapcsoljuk a tárcsát a „stopperóra”, ha a labda (henger) nem kapcsolja ki az időzítőt, ismételje meg a tapasztalat. Távolítsuk el a stopperórát számlálási idő t a labda mozgását (henger).

6. § 3-5 ismétlés 5 alkalommal.

7. Számítsa az átlagos idő gördülő.

8. Place egy átlagos idő a (20) képletű. Keresse kísérleti tehetetlenségi nyomatéka a labdát (henger).

10. Számítsuk ki az abszolút és relatív hiba képletekkel:

egy henger és egy gömb.

11. A következtetés a munka.

tesztkérdések

1. Mit nevezünk forgómozgást?

2. Mi a neve a pillanatban az erők?

3. által meghatározott tehetetlenségi nyomatéka az anyag pont m tekintetében a forgási középpont, egymástól bizonyos távolságban r?

4. Mi határozza meg a tehetetlenségi nyomatéka a test?

5. Írja képletű tehetetlenségi nyomatéka a henger, egy olyan tengely körül nem halad át a forgatás középpontjának.

6. Írj egy formula, amely meghatározza a teljes mechanikai energia a test, amikor a gép mozgás?

7. Valamely képletű határoztuk tehetetlenségi nyomatéka a henger (tálban) empirikusan?

8. Egyes képletű határoztuk tehetetlenségi nyomatéka a henger (tálban) egy elméleti?

9. Kap egy képletet a gyorsulás a tömegközéppontja a labdát gördülő a ferde sík, a törvény az energiamegmaradás.

irodalom

1. A kurzus a fizika. At 3 m. T. 1. Mechanics. Molekuláris fizika. - M. Science 1989.

2, stb -. M. Executive. wk. 1980

3., stb -. M. Oktatási, 1985.