Megoldása lineáris programozási feladatok grafikusan
Definíció. Minden olyan döntést a rendszer által a megszorítások nevezzük megvalósítható megoldást ZLP.
Definíció. Egy érvényes megoldás, amelynek során a célfüggvény eléri a maximális vagy minimális értéket nevezzük az optimális megoldást.
E meghatározások LP probléma az alábbiak szerint történik: a minden pont a konvex tartománnyal, amely egy olyan megoldás, a rendszer korlátai, hogy kiválassza az ilyen koordinátákat, amelyek minimalizálják a (maximalizálása) a lineáris függvény F = + s1x s2y.
Figyeljük meg, hogy az x változó. y ZLP hogy általában nem negatív értékeket (x ≥ 0, y ≥ 0), így a régió található, az I. negyedévben koordinátasík.
kép
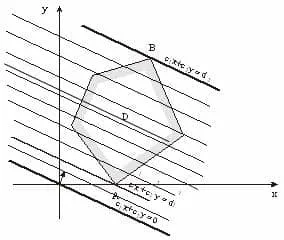
Módosítása a rögzített értéket F = d. egyenes s1x s2y + = d elmozdul párhuzamosan és „zachertit” egész gépet. Legyen D - poligon - egy olyan terület korlátozása rendszer megoldások. Ha megváltoztatja a D vonal s1x s2y + = d. Néhány értéke d = d1 D. eléri ezt a pontot nevezzük a sokszög A „belépési pont”, majd miután elhaladtak egy sokszög, valamilyen értéke d = d2 lesz vele az utolsó közös pont az úgynevezett V. A „kilépési pontot.”
Nyilvánvaló, hogy a legkisebb és legnagyobb értékét a célfüggvény F = + s1x s2y eléri a pontot az „input” A és „kilépés” B.
Tekintettel arra, hogy az optimális érték a sor lehetséges megoldás célfüggvény veszi át a csúcsai D. javaslatot tehet a következő terv döntés ZLP:
- építeni területe korlátozások a megoldások;
- építeni egy megfelelő sorban célfüggvény, és párhuzamos fordítás ebben a sorban találni egy pont a „belépési” vagy az „exit” (igényeitől függően, hogy minimalizálják vagy maximalizálja a célfüggvény);
- koordinátáinak meghatározására a pontot, akkor értékének kiszámításához a célfüggvény.
Megjegyezzük, hogy a vektor (c1. C2) merőleges az egyenes vonal mutatja az irányt a növekedés a célfüggvény.
Abban grafikus megoldás ZLP két lehetséges esetet, hogy különös megfontolást igényel.
1. eset

6. ábra
Amikor a mozgó egyenes s1x s2y + = d «bejárat” vagy »kilépés« (mint látható) fordul elő az oldalán a sokszög. Ez történik, ha a sokszög oldalai párhuzamosak a vonal + S1H s2u = d.
Ebben az esetben a pontok „exit” ( „input”) számtalan - azaz bármely pontján az AB szakasz. Ez azt jelenti, hogy a cél a függvény feltételezi a maximális (minimális) érték nem egy ponton, és minden ponton, amely megfelelő oldalán a sokszög D.
2. eset
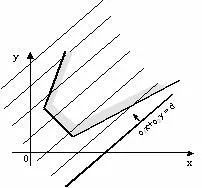
Vegyük azt az esetet, amikor a különböző megengedett értékeket korlátlan.
Abban az esetben, kötetlen régió a célfüggvény lehet meghatározni úgy, hogy a „kimenet” (vagy „belépési”), amely megfelel ennek nincs közvetlen pont. Ezután a maximális érték (minimum) nem érik el soha - azt mondják, hogy a funkció nem korlátozott.

kép
Meg kell találni a maximális érték a célfüggvény F = 4x + 6Y → max. amikor a rendszer korlátai
Készítünk egy megvalósítható régióban, azaz a grafikusan megoldani egyenlőtlenségrendszer. Erre építünk minden sor, és meghatározza a félig által meghatározott sík egyenlőtlenségeket.
x + y = 18
Construct megfelelő sorban függvény F érték = 0. 4x + 6Y = 0. Azt fogja mozgatni a vonal párhuzamos módon. Az összes családok sor 4x + 6Y = const utolsó csúcs, amelyen keresztül adja át közvetlenül a kilépés a sokszög határán lesz a tetején a C (12, 6). Itt van, hogy F = 4x + 6Y eléri a maximális értéket.
Ezért, ha x = 12, y = 6, az F függvény eléri a maximális értéket az F = 4 # 8729; 12 + 6 # 8729; 6 = 84, egyenlő 84. A pont koordinátái (12; 6) kielégíti az összes rendszer korlátai egyenlőtlenségeket, és ez az érték a célfüggvény optimálisan F * = 84 (az optimális érték lesz jelöljük „*”).
A probléma megoldódott. Tehát szükség van, hogy kiadja 12 termék I. típusú és a 6. típusú termékek, a nyereség 84 ezer. Rub.
A grafikus módszert használják, hogy megoldja a problémákat, hogy már csak két változó rendszer korlátait. Ez a módszer alkalmazható rendszerek egyenlőtlenségek, három változóval. Geometriailag a helyzet más lesz a szerepe játszott közvetlen sík háromdimenziós térben, és az oldatot a egyenlőtlensége három változó lesz egy fél hely, egyik oldalán helyezkedik el a gépet. A régiók szerepe fog játszani egy poliéder metszéspontjában félig terek.
Szabályok adatbevitel
Kérdezzen, vagy hogy észrevételeit, javaslatait lehet az oldal alján a részben Disqus.
Ön is küldhet egy kérést segítséget foglalkozó vizsgálatok a megbízható partner (itt és itt).