Menetrend tangens algebra

Hogyan építsünk egy függvény grafikonját az y = tg x? Először is, úgy a grafikon az érintő az intervallum (- π / 2; π / 2).

A szám π kerekítve a legközelebbi egész:

Vegye egység intervallum hossza 2 sejtek notebook. Ebben az esetben, a száma π megfelel a szegmens hossza 6 sejtek száma, a π / 2 - 3-sejtek, π / 6 - 1 sejt, π / 4-1,5-sejtek, π / 3 - 2 sejtek.

A domain a funkció y = tg x nem tartalmazza a számát

érintőlegesen a grafikon függőlegesek aszimptotákkal, a grafikon kell törekedni, de soha nem éri el. Aszimptota szokás szaggatott vonalak.

Készítsünk egy táblázatot a tan értékek a [0; π / 2):

A koordinátasík ünnepli a kapott pontok és aszimptota.

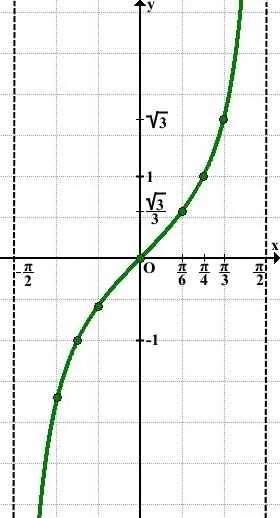
Mivel a függvény a tg x - periódusidővel T = π, a tangense a grafikon, hozott az intervallum (-π / 2; π / 2) megismételjük, hogy a bal és a jobb a plusz és mínusz végtelen:

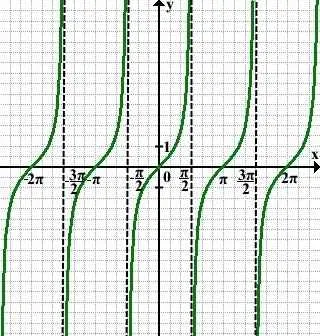
A grafikon y = tg x

A grafikonok a funkciók, többek között trigonometrikus, algebra lehet használni, hogy megoldja egyenletek, egyenlőtlenségek, a megoldás más feladatokat.