Optimalizálási módszerek egy túlméretezett a probléma
Bomlás alapú aggregációs eljárás egy nagyszabású problémák
összesítésével bomlási módszert nemlineáris programozási feladatok
bomlás rendszerek
Az elv bomlás (vagy ahogy nevezik, decentralizáció elve) az, hogy partíció a rendszer alrendszerekre kívánt tulajdonságú. Ezt a módszert használják igazolás hierarchikus építési komplex rendszerek, különösen a tanulmány a különböző minták közötti kölcsönhatás szintek közötti szint gazdasági rendszerek megoldására operatív ellenőrzése és ütemezési feladatokat.
Az alkalmazás a problémák bomlás a optimalizálás particionálni a fő feladat a részfeladatok lényegesen kisebb méret, amely lehet megoldani a meglévő eszközökkel.
Ezek részfeladatok alkotják az első hierarchikus rendszerben létrehozott számítógépes célra.
Az első szinten részfeladatok megoldódnak tetszőleges kapcsolatokat. Meghatározása e kapcsolatok a feladata a második szintre.
Nincs központi ellenőrző szerv részletes információkat termelési képességeit az egyes alrendszerek szükségessé egy hierarchikus struktúrát, amelyben a szülő szervezet gyűjt egyes aggregált információkat alárendelt alrendszerek, majd elengedi az egyik vagy másik jele a kívánt vagy várt tevékenységüket. Miután elolvasta ezeket az utasításokat, az alrendszer tudja irányítani a felső „counter-tervek”, amelyben a legjobb módja az általuk figyelembe venni az érdekeiket.
A fenti információk alapján, a központi test igazítja útmutatást, és a folyamat addig ismétlődik, amíg a végleges megállapodás.
A megkülönböztető jegye a sok gyakorlati problémát a kutatás a nagy léptékű. Különösen, amikor a problémák megoldásához optimális tervezése makró korlátok mátrix dimenziójával eléri a 10 4 -10 5. Ebben a dimenzióban a klasszikus matematikai programozási módszerek (lineáris, nemlineáris, diszkrét) hatástalanok. Ie állunk szemben itt a jelenség „átok dimenzionalitás” megértés R.Bellmana.
Ez szükségessé tette a fejlesztés speciális technikák, mint a pontos és közelítő szánt nagyméretű problémákat. A legtöbb ilyen módszer ötletét használja bomlás, ami feldarabolása az eredeti probléma nagyméretű, megállapítva, független megoldások mindegyike majd kapcsolni ezeket a különös megoldást az általános megoldás az eredeti probléma. Az az elképzelés, bomlás tekintetében a LP probléma már megfogalmazott G.Dantsigom és Wolf, és később kifejlesztett D.B.Yudina, B.G.Golshteyna [12] M. Mesarovich, L.Lesdona [31] V.Tsurkova [52], és mások.
A bomlási módszer Dantzig-Wolfe
G. Danzig 1960-ban, és Wolfe bomlási módszert fejlesztettek megoldások nagy dimenziós problémák egy speciális szerkezet a korlát mátrix [31].
Ez a módszer a leghatékonyabb a problémák megoldására, megszorítás mátrix, amely egy blokk-diagonális formát egy kis változók száma. Azonban, amint azt a további kutatás, a módszer is alkalmazható LP problémák általános mátrix formájában. A megfelelő eljárást hoztunk D.B.Yudinym és E.G.Golshteynom úgynevezett „blokk programozás” [12].
A megkülönböztető jegye a bomlás módszer használata a koordinációs feladat. amely, mint az eredeti, kis számú vonalak és a nagy számú oszlopot.
Lényeges, hogy ez nem szükséges megadni az összes oszlopot kifejezetten, hogy foglalkozzon a koordinációs problémát. Ezek keletkezett a folyamat, amelynek során a szimplex módszer. Ez a megközelítés az úgynevezett oszlopon generációs módszer. Ennek lényege a következő. Legyen LP probléma típusok:
Tegyük fel, hogy megengedhető ismert bázikus oldat (DBR) XB és a megfelelő mátrix alapján vektorovA. Tételezzük fel továbbá, hogy az XB találtak a fordított mátrixba. Aztán ott találtak egy időben, és a vektor relatív értékelés
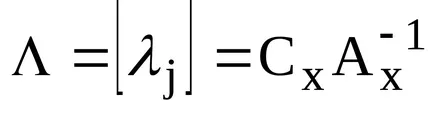
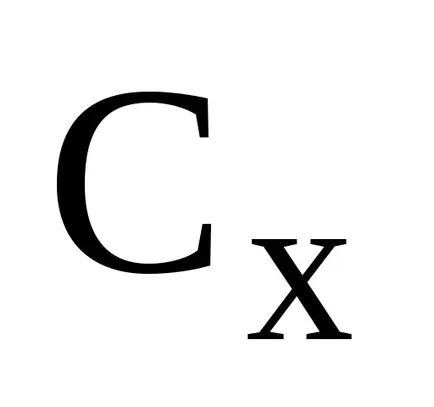
Ahhoz, hogy meghatározzuk a javításának lehetőségét a XB DBD az egyes nem-bázikus vektoraAj számított értékelési érték:
Ha a kezdeti oldatot javítható bevezetésével változó alapú XS. Azonban, ha van egy nagy számú nem-bázikus oszlopok (n10 3) által nahozhdenieS vychisleniyaj vektorok minden nem-bázikus
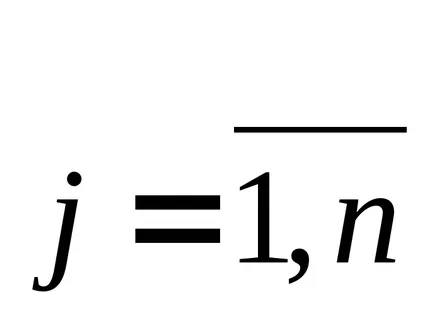
Feltételezzük, hogy az összes oszlopot AS választott konvex mnozhestvaS. meghatározott rendszer és egyenlőtlenségek. Ezután az oszlopot vektor be kell vinnie alapján lehet meghatározni megoldásával kiegészítő probléma a következő formában:
ahol
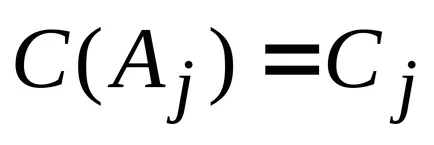
Egy ilyen folyamatot nevezzük az oszlop generáció. mivel a probléma megoldása (4) valójában csak egy kis számú oszlop keletkezik, ha szükséges.
Ez jelentősen csökkenti a szükséges memória kapacitása tárolására a jelenlegi teljesítmény, ami jelentős előny a megoldására nagyszabású problémákat.