Példa a rajzoló funkciókat meghatározott implicit

Tekintsük a rajzoló funkciókat a következő példa:

Példa. Postroimt grafikon \ (x \, hogy y (x) \), meghatározott implicit, a paraméter schetaete pozitív \ (a> 0 \). $$ x ^ 4 + y ^ 4 = a ^ 2 (x ^ 2 + y ^ 2) $$
Határozat. A vizsgálat a függvény grafikon és a kivitelezést annak Keypoint. Nyilvánvaló, hogy a függvény grafikonját szimmetrikus a koordinátatengelyek, azaz lesz, hogy végezzen kutatást menetrend az első negyedévben, azaz a \ (x \ GEQ 0 \) és \ (y \ GEQ 0 \). A funkció meghatározott és folyamatos az összes \ (x \). Ábrázoljuk a görbe paraméteres formában, cserélje \ (y = tx \). mert megvizsgálunk egy görbét az első chetveti, majd \ (y \ GEQ 0 \). Behelyettesítve 4 $$ x ^ + y ^ 4 = a ^ 2 (x ^ 2 + y ^ 2) => x ^ 4 + (TX) ^ 4 = a ^ 2 (x ^ 2 + (TX) ^ 2) = > $$$$ x ^ 2 + t ^ 4x ^ 2 = a ^ 2 (1 + t ^ 2) => x ^ 2 = a ^ 2 \ frac<1+ t^4> = X = A \ sqrt<\frac<1+ t^4>> $$ helyettesítheti az egyenlet \ (y \) $$ y = tx => y = t a \ sqrt<\frac<1+ t^4>> $$ Compute származékok \ (x '\) és \ (y' \) $$ x „= (a \ sqrt<\frac<1+ t^4>>) '= \ Frac \ sqrt> \ frac' = A \ sqrt> \ frac $$ egyenlővé az első derivált a 0, és megtalálja a stacionárius pontok $$ x „= A \ sqrt> \ frac = 0 => t (1 - 2T 2 ^ -t ^ 4) = 0 => t_1 = 0, t_2 = \ sqrt $$ meghatározzák a jele a származék a környező ezeket a pontokat, megkapjuk

kapnak, azon a ponton, \ (t = \ sqrt; x = a \ frac; y = a \ sqrt> \) deriváltja elõjelet a + a - azaz a Ez a pont a maximális
meg kell határozni a metszéspont a tengellyel \ (y \), a tengely \ (x \) már - szélsőséges. \ (X = 0, x ^ 4 + y ^ 4 = a ^ 2 (x ^ 2 + y ^ 2) => y ^ 4 = a ^ 2y ^ 2 => y = a \)

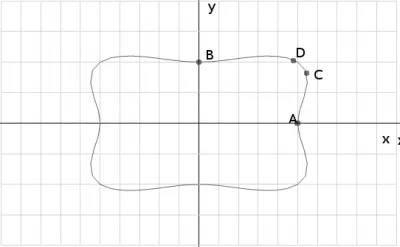
Alkalmazzuk a pont a derékszögű koordináta rendszerben, össze egy görbe az első chetvetri, majd térképen is szimmetrikusan a tengelyre \ (Ox \), majd a \ (Oy \), és így a következő reschultat