Quantum oszcillátor - studopediya
Klasszikus oszcillátor klasszikus mechanika úgynevezett részecsketömeg m. frekvenciával oszcillál W0 =Ök / m a rugalmas erő révén F = -kx.
A potenciális energia ilyen részecskék U = kx 2/2 = mx 2/2; koordinátákra ± hmax egyenlő a teljes energia E. Így részecske energia bármilyen értéket felvehet, azaz folyamatosan változhat (6. ábra).
A kvantummechanikában a koncepció erő nem használható, így a kvantum oszcillátor kell meghatározni, mint egy részecske egy potenciális energia U = kx 2/2 = mx 2/2. (34)
Behelyettesítve (34) be (22), valamint figyelembe véve, hogy a részecske mozog csak egy egyenes mentén (az x tengely mentén), megkapjuk
Megoldása (35) egyenlet állíthatjuk elő, hogy az energia (energia szinten) a részecske feltételezi csak diszkrét értékeket (kvantált).
n = 0, 1, 2 - a kvantum számokat.
A legkisebb energia értéke E0 = W0 / 2 esetben csak a természetes frekvencia W0, és nem elvenni részecskéket lehűtjük, azt is meg kell őrizni, és a T = 0K.
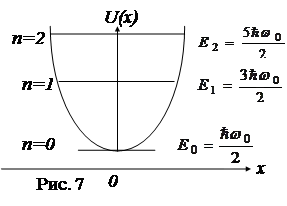
azaz egyenlő távolságra szintet [lásd. Ábra. 7, ahol a határ a lehetséges görbe U (± Hmax) = En]. Magasabb kvantumszámok n DE / En = 1 / (n + 1/2) ®0. azaz konvergencia lép fel viszonylagos energiaszintet és a kapott eredmények közel állnak a klasszikus kezelést, amikor az energia a részecske folyamatosan változtatható, és ezért bármilyen értéke. Ez az elv a levelezés. által megfogalmazott Bohr 1923-ban.:
A nagyméretű kvantumszámok a megállapítások és eredmények kvantummechanika meg kell felelnie a következtetések és eredmények a klasszikus mechanika.
Egy általánosabb értelmezése a levelezés elv a következő: minden új, általános elmélet fejlődésének klasszikus, nem utasíthatja el teljesen, és magában foglalja a klasszikus elmélet, rámutatva, hogy annak használata külföldön. Sőt, bizonyos szélsőséges esetekben az új elmélet lesz a régi.
11. fizika előadás atomok és molekulák