Rotor (matematika), a virtuális laboratórium wiki, rajongók powered by Wikia
Rotor. vagy elfordulás - vektor eltérés operátor a vektor mezőt. Ez azt mutatja, hogy mennyi és milyen irányban forog területén minden ponton. mező F forgórész jelöljük rothadás F (az orosz irodalomban), vagy curl F (angol irodalomban), és ahol - a vektor differenciáloperátor nabla.
A matematikai definícióját a megfelelő
A rotor egy vektor mező - vektor, amelynek vetítési minden irányban egyenlő a határ aránya forgalomban egy vektor mező a kontúr L sík terület? S, merőleges erre az irányra, hogy az értéke ezen a területen, ha a méret a terület általában nulla, és maga a weboldal is zsugorodik, egy pont:
.
Normál, hogy a helyszínen irányul úgy, hogy a számítás a cirkulációs kör a kontúr L, az óramutató járásával ellentétes.
A háromdimenziós Descartes-féle koordináta-rendszer a következőképpen kell kiszámítani:
Az egyszerűség kedvéért, akkor tárolja a hagyományosan képviselik a forgórész vektoros termék.
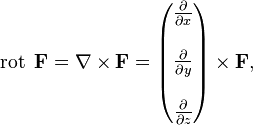
vagy mint a meghatározó a következő mátrix:
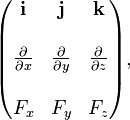
A vektor a területen, a rotort, amely a nullával egyenlő bármely pontján az úgynevezett potenciális (lehessen beállítani).
A fizikai szabályok értelmezése
Szerint a Cauchy-tétel Helmholtz-folytonos közegben sebességeloszlás közelében az O pont a következő egyenlet adja
ahol - a vektor a szögelfordulás a közeg elem az O pont, és - a kvadratikus alak a koordináták - a lehetséges az közeg elem deformáció.
Így, a mozgás a folyamatos közeg közelében az O pont áll transzlációs mozgást (vektor), a forgómozgás (vektor) és a lehetséges mozgás - törzs (vektor). Alkalmazása a Cauchy Helmholtz rotor működését, azt látjuk, hogy az O pont az egyenlőség és így megállapíthatjuk, hogy mikor jön a vektor mező mező egy közepes sebességgel, a rotor e vektor mező egy adott ponton a kétszeresével egyenlő szögelfordulás közepes elem központ ezen a ponton.
Például, ha a vektor mezőt, hogy a területen a szélsebesség a világon, akkor a ciklon. jobbra forog. A rotor lefelé mutat, és a ciklon, forgó óramutató járásával ellentétes irányban - felfelé. Azokon a helyeken, ahol a szelek fúj egyenes vonalúan és azonos sebességgel, a forgórész lesz egyenlő nulla (y inhomogén lineáris áramlási rotor nem nulla).
Alapvető tulajdonságait szerkeszthetjük
A következő tulajdonságok érhetők el a hagyományos levezetési szabályok.
- Ha - a skalármező, és az F - vektor, akkor:
- A divergencia a rotor nulla:
Ebben az esetben az ellenkezője igaz: ha a mező F egy divergenciamentes, ez a terület egy örvény területén G.
- Ha az F mező lehetséges, a rotor nulla (F területén - lehessen beállítani):
Ezzel szemben, ha a mező lehessen beállítani, potenciálisan:
Néhány skalármező
- Stokes-tétel. vektor forgalomban zárt áramkör, amely egy határoló felület, ez a vektor egyenlő az átfolyást a felületén a rotor:
Rotor ortogonális görbe vonalú koordináták szerkesztése
példák szerkesztése
Egyszerű vektor mező szerkesztése
Tekintsük a vektor mezőt. lineárisan függ a koordinátái x és y.
.
Nyilvánvaló, hogy a mező forog. Ha tesszük a lapátkerék bármely területén területen, azt látjuk, hogy kezd forogni az óramutató járásával megegyező irányban. A jobb kéz szabályt. várhatóan be lehet csavarni az oldalon területen. Egy jobbkezes koordináta-rendszerben az irányt az oldalt jelent majd negatív irányba a Z tengely mentén.
Ahogyan azt iránya egybeesik a negatív Z tengelyre. Ebben az esetben a forgórész állandó mivel ez független a koordináta. Az összeg a forgás a fenti vektor mező azonos bármely ponton (x, y). rotor Graph F nem nagyon érdekes:
Egy bonyolultabb példa szerkesztése
Most tekintsünk egy kicsit bonyolultabb vektor mező:
.
Nem látunk semmilyen forgatás, de akik közelebb a jobb, azt látjuk, egy nagyobb területen, például az x = 4, mint az x = 3. Ha telepíteni egy kis lapátkerék van, nagyobb áramlási jobb oldalán okozna a kerék forog az óramutató járásával megegyező irányban, amely megfelel a csavarozás irányba -z. Ha helyeztük a kereket a bal oldalán a területen, nagyobb áramlási hogy a bal oldali okozna a kerék forog az óramutató járásával ellentétes irányban, ami megfelel a becsavarási irányban + z. Mi ellenőrizzük az felbecsülni:
Valóban, van csavarva a + Z irányba, hogy a negatív X és -z pozitív x. mint várták. Mivel a rotor nem azonos minden ponton, a menetrend egy kicsit érdekes:
Látható, hogy a grafikon a forgórész nem függ Y vagy Z (mint amilyennek lennie kellene), és a mentén irányul -z pozitív x és + Z irányban negatív x.
Három gyakori példa szerkesztése
Tekintsük a példát # 8711; × [V × F]. Egy derékszögű koordináta-rendszert, meg tudjuk mutatni, hogy
Ha v és # 8711; csere:
ez egy Feynman rekord alacsonyabb index # 8711; F. ami azt jelenti, hogy a gradiens-index F csak a F.
egy másik példa # 8711; × [ # 8711; × F]. Egy derékszögű koordináta-rendszert, meg tudjuk mutatni, hogy:
amely lehet tekinteni egy speciális esete az első példa, a helyettesítése v → # 8711;.
Szemléltető példák szerkesztése
- A tornádó szél körül forognak a központ, és a szél sebessége vektor mező lenne nullától középpontjában a forgórész és esetleg máshol. (Lásd. Örvénylő mozgásban).
- A vektor mezőt, amely leírja a lineáris sebessége egyes pontja a forgó tárcsa forgórész lenne állandó minden részén a lemezt.
- Ha a sebesség az autók a pályán által leírt vektor mező, és a különböző zenekarok különböző korlátozásokat mozgási sebessége a rotor van a határ a sávok között lenne nulla.
- Faraday indukciós törvénye. egyik Maxwell-egyenletek. Fejezhető ki nagyon egyszerűen át a rotor fogalom. Azt mondja, hogy a forgórész az elektromos mező egyenlő a változás sebessége a mágneses mező ellentétes előjelű, és a forgórész mágneses térerősség az összege áramsűrűség és a normál előfeszítő áram.
Megjegyzések szerkesztése
- ↑ szótár Matematikai középiskolában. V.T.Vodnev, A.F.Naumovich, N.F.Naumovich