Számos forgalmazás

Ennek során a fejezetet szentelt az alapvető fogalmak valószínűségszámítás, mi vezetett a nagyon fontos fogalom a véletlen változó. Itt adunk további fejlődését ez a fogalom, és jelzik, milyen módon véletlen változók leírható és jellemezni.

Mint már említettük, a véletlen mennyiség olyan mennyiség, amely tapasztalat eredményeként vehetnek egyik vagy másik értéket, előre nem ismert -, hogy melyik. Abban is megállapodtunk, hogy különbséget véletlen velichinypreryvnogo (diszkrét) és folyamatos jellege. Lehetséges értékek folytonos értékek felsorolt ​​előre. Lehetséges értékek folyamatos értékek felsorolt ​​előre és folyamatosan tele bizonyos intervallumon.

Példák folytonos valószínűségi változók:

1) az előfordulások számát a jelkép három dob érmék (lehetséges érték 0, 1, 2, 3);

2) A megjelenés gyakorisága az embléma az ugyanabban a kísérletben (a lehetséges értékek);

3) a számos sikertelen elemek egy eszközhöz, amely öt elem (lehetséges érték 0, 1, 2, 3, 4, 5);

4) a találatok száma egy olyan síkban, amely elegendő ahhoz, hogy ki hatását (lehetséges értékek 1, 2, 3, ..., n, ...);

5) légi járművek száma a levegőben csatában lezuhant (lehetséges érték 0, 1, 2, ..., N, ahol - az összes érintett repülőgépek a csatában).

Példák folytonos valószínűségi változók:

1) abszcisszán (ordináta) az ütközési pont a lövés;

2) a távolság a ütő pont a központ a cél;

3) a hiba méteres magasságot;

4) üzemidő rádiólámpák.

A továbbiakban a véletlen változók jelöli betűvel, és azok lehetséges értékeit - megfelelő kisbetűkkel. Például - a találatok számát három lövést; lehetséges értékei.

Tekintsük folytonos véletlen változó lehetséges értékei. Mindegyik értékek is lehetséges, de nem jelentős mértékben, és az X változó vehet mindegyikük bizonyos valószínűséggel. Ennek eredményeként az X érték fog tapasztalni egy ilyen értékeket, azaz előfordulása az egyik teljes csoport összeférhetetlen események:

Jelöljük a valószínűsége ezek az események p betűt a megfelelő indexek:

Mivel a nem kompatibilis események (5.1.1) alkossanak csoportot,

azaz az összeg a valószínűségek minden lehetséges véletlen változó értéke egyik értékeket. Ez a teljes veroyatnostkakim elosztott módon az egyes értékeket. Egy véletlen változó teljesen le van írva a valószínűségi szempontból, ha megkérdezzük ezt az eloszlást, azaz Pontosan meghatározza, hogy milyen valószínűséggel van minden esemény (5.1.1). Ily módon létrehozza az úgynevezett törvénye eloszlás valószínűségi változó.

véletlenszerű értékek eloszlása ​​törvény bármilyen arányú létrehozó kapcsolat a lehetséges értékek valószínűségi változó és a megfelelő valószínűségek. Mintegy véletlen változó, azt fogja mondani, hogy ez vonatkozik az eloszlási törvényt.

Létrehoz egy formája, amelyben a forgalmazási jog folytonos véletlen változó lehet beállítani. A legegyszerűbb formája a feladatot a törvény egy táblázat, amely felsorolja a lehetséges znacheniyasluchaynoy értékek és a hozzájuk tartozó valószínűségeket:

Ez a táblázat fogják hívni a következő véletlen változó.

Ahhoz, hogy egy szám eloszlás perspektivikus nézetben, gyakran folyamodnak a grafikus ábrázolás: a vízszintes tengelyen a lehetséges értékek valószínűségi változó, és a függőleges tengelyen - ezek valószínűségi értékek. Az érthetőség kedvéért, az adatpontok vannak összekötve vonalszakaszok. Ez a szám az úgynevezett egy sokszög eloszlása ​​(ábra. 5.1.1). Sokszög eloszlása, valamint a száma eloszlások teljesen jellemzi a valószínűségi változó; ez egy forgalmazási forma.

Néha kényelmes úgynevezett „mechanikus” értelmezése számos forgalmazás. Képzeljük el, hogy egy kis tömege megfelel az egység, eloszlik az abszcisszán, úgy, hogy az egyes pontok rendre koncentrált tömeg. Ezután több elosztó értelmezi a rendszer lényeges pontokon néhány tömegek található az x tengelyen.

Tekintsük néhány példa a folytonos valószínűségi változók eloszlása ​​törvényeket.

1. példa termel egy élmény, amely akkor kaphat, vagy nem kapja meg az eseményt. A valószínűsége egy esemény 0,3. Úgy véljük, egy véletlen értéket - az előfordulások számát esemény ebben a kísérletben (azaz a véletlen változó jellemző eseményeket figyelembe véve a értéke 1, ha az megjelenik, és 0, ha nem jelenik meg.). Construct forgalmazásával sorozat és poligon a forgalmazás.

Határozat. Az érték csak két értéket 0 és 1 több elosztó értékek:

Sokszög eloszlás ábrán látható. 5.1.2.

2. példa termel három lövő tüzelési egy cél. Annak a valószínűsége, ütő a cél minden lövés 0.4. Minden hit szerzett 5 pontot nyíl. Készítsük el a forgalmazás sorozat dombornyomott pont.

Határozat. Számát jelöli a knock-out pont. Lehetséges értékek nagyságrendekkel. .

Annak a valószínűsége, ezek az értékek olyan ismétlési tétel kísérletek:

Több eloszlása ​​a következő:

Sokszög eloszlás ábrán látható. 5.1.3.

3. példa: a valószínűségét egy esemény egy kísérlet. Elkészítette független kísérletek, amelyek továbbra is csak az első előfordulása esetén. ami után a kísérletek megszűnik. Véletlen változó - a vizsgálatok száma tette. Készítsük el a forgalmazás sorozat értékét.

Határozat. Lehetséges értékek nagyságrendekkel. 1, 2, 3, ... (elméletileg nem korlátozott). Ahhoz, hogy elfogadott érték értéke 1, az szükséges, hogy egy esemény történt az első kísérletben; ennek a valószínűsége is. Ahhoz, hogy értéket vett értéke 2, meg kell először megtapasztalják az esemény nem jelenik meg, és a második - megjelent; ennek a valószínűsége is. hol. stb Több eloszlása ​​a következő:

Az első öt-ordináta a eloszlása ​​sokszög az ábrán bemutatott esetben. 5.1.4.

4. példa A lövő forgat egy cél, hogy az első érintkező, amelynek négy lőszer patront. Veroyatnostpopadaniya minden lövés 0.6. Készítsük el a forgalmazás sorozat lőszert, a megmaradt, felhasználatlan.

Határozat. Véletlen érték - száma el nem költött kazetták - négy lehetséges értékei: 0, 1, 2 és 3. A valószínűségek ezek az értékek rendre egyenlő:

Több eloszlása ​​a következő:

Sokszög eloszlás ábrán látható. 5.1.5.

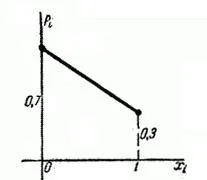
5. példa technikai eszköz lehet használni a különböző körülmények között, és attól függően, hogy időről időre szükség kiigazítás. Egyetlen eszköz használata akkor véletlenszerűen esnek kedvező vagy kedvezőtlen módban. készülék kialakít három alkalmazás beállítása nélkül A kedvező módban; a negyedik előtt kell beállítani. A hátrányos helyzetű módban a készülék ki kell igazítani az első használat után. Annak a valószínűsége, hogy a készülék kap egy kedvező bánásmód - 0,7, ami kedvezőtlen - 0.3. Úgy véljük, egy véletlen érték - a kérelmek száma állítsa be a készüléket. Építsd a több elosztó.

Határozat. Egy véletlen változó három lehetséges értékek: 1, 2 és 3. Annak a valószínűsége, hogy a. annak a valószínűsége, hogy az első kérelem eszköz kap egy kedvezőtlen mód, azaz a . Ahhoz, hogy elfogadott érték értéke 2, az szükséges, hogy az első alkalmazás berendezésnek van egy kedvező módja, és a második - a kedvezőtlen; A valószínűsége ennek. Ez az összeg az elfogadott értéke 3, akkor kell első két alkalommal a termék már kedvező kezelés után (a harmadik alkalommal viszont továbbra is be kell állítani). Annak a valószínűsége, ez.

Több eloszlása ​​a következő:

Sokszög eloszlás ábrán látható. 5.1.6.

Az előző n °, vezettünk be több elosztó, mint egy átfogó válasz (forgalmazás törvény) nem folytonos véletlen változó. Azonban ez a funkció nem általános; ez létezik, csak a folytonos valószínűségi változók. Könnyen belátható, hogy az nepreryvnoysluchaynoy értéke ilyen jellemzőkkel nem lehet építeni. Valóban, a folytonos véletlen velichinaimeet végtelen számú lehetséges értékek, teljesen kitöltve egy bizonyos ideig (az úgynevezett „megszámlálható halmaz”). Hozzon létre egy táblázatot, amely felsorolja az összes lehetséges értéke egy véletlenszerű változó, lehetetlen. Továbbá, amint az az alábbiakból látható, minden egyes érték egy folytonos valószínűségi változó általában nincs nulla a valószínűsége. Következésképpen, egy folytonos valószínűségi változó, nincs sorozat eloszlás abban az értelemben, hogy létezik a szakaszos értéket. Azonban a különböző régiókban a lehetséges értékek valószínűségi változó még nem egyformán valószínű, és van egy „valószínűségi eloszlás” a folyamatos mennyiség, de nem abban az értelemben, mind a folytonos.

Számszerűsíteni a jellemzői a valószínűség-eloszlás kényelmesen használható hihetetlen esemény. és a valószínűsége esemény. ahol - néhány aktuális változó. Veroyatnostetogo események nyilvánvalóan függ. függvénye. Ez az úgynevezett véletlen változó eloszlás és jelöljük:

Az eloszlásfüggvény néha nevezik eloszlásfüggvény vagy kumulatív eloszlás törvény.

eloszlásfüggvény - a leguniverzálisabb jellemzőit valószínűségi változók. Ez létezik az összes véletlen változók: hogyan szakaszos és folyamatos. Az eloszlásfüggvény teljesen harakterizuetsluchaynuyu értéket a valószínűségi szempontból, azaz Ez egy formája a forgalmazás.

Megfogalmazzuk néhány általános tulajdonságait az eloszlásfüggvény.

1. Az eloszlás függvény csökkenő függvénye az érvelését, vagyis címen.

2. A mínusz végtelen, az eloszlásfüggvény értéke nulla :.

3. A plusz végtelenben, az eloszlásfüggvény értéke egy :.

Anélkül, hogy egy szigorú bizonyítás Ezen tulajdonságok illusztráljuk őket vizuális geometriai értelmezést. Ehhez figyelembe vesszük a valószínűségi változó, mint egy véletlen pont az x tengelyen (ábra. 5.2.1), amely a tapasztalatok eredményeképpen a eltarthat egyik vagy másik helyzetbe. Ezután az eloszlásfüggvény estveroyatnost, hogy egy véletlen pont eredményeként a tapasztalat lesz a bal oldali pont.

Mi fog növekedni. t. e. mozgatni a lényeg, hogy a közvetlenül a vízszintes tengely. Nyilvánvaló, hogy a valószínűsége, hogy egy véletlenszerűen kiválasztott ponton esik a bal oldalon. nem lehet csökkenteni; ezért az eloszlás egyre csökken nem.

Annak érdekében, hogy. Mi lesz a végtelenségig mozgatni a lényeg, hogy a bal oldalon a vízszintes tengely mentén. Így a véletlen bejutása pontot balra a határ lehetetlenné válik esemény; Természetesen feltételezhetjük chtoveroyatnost ez az esemény nullához, azaz .

Hasonlóképpen korlátozás nélkül azáltal, hogy a pont a jobb, azt látjuk, hogy. az esemény jelentőssé válik a határ.

A grafikon az eloszlási függvény az általános esetben egy nemcsökken˝o függvény grafikon (ábra. 5.2.2), az értékeket, amelyek indulnak 0 és megy akár 1, azzal jellemezve, diszkrét pontokon lehet a funkciója ugrik (folytonossági).

Ismerve száma folytonos eloszlása ​​egy valószínűségi változó, akkor könnyen építeni ezt az értéket eloszlásfüggvény. Tény, hogy

ahol az egyenlőtlenség alapján az összegzés tábla jelzi, hogy az összegzés kiterjed az egész értékeket. amelyek kevésbé.

Amikor az aktuális változó áthalad néhány lehetséges nagyságát folytonos értékeket. eloszlásfüggvény hirtelen nagymértékben megváltozik, és a nagysága a folytatásban egyenlő a valószínűsége, hogy ez érték.

1. példa termel egy élmény, amely akkor kaphat, vagy nem kapja meg az eseményt. A valószínűsége egy esemény 0,3. Véletlen változó - az előfordulások számát az esemény a tapasztalat (a belső értéke egy véletlen esemény). Építeni a eloszlásfüggvény.

Határozat. Több eloszlása ​​a következő:

Építünk értékét az eloszlásfüggvény:

A grafikon az eloszlási függvény ábrán látható. 5.2.3. A pontokat a diszkontinuitás veszi jelölt értékek pontok az ábrán (bal folytonos függvény).

2. példa A körülmények az előző példa 4 független kísérlet eredményének. Construct eloszlásfüggvénye az előfordulások számát az esemény.

Határozat. Jelöljük - az előfordulások számát az esemény négy kísérletben. Ez az érték számos elosztási

Készítünk egy véletlen változó funkció:

A grafikon az eloszlási függvény ábrán látható. 5.2.4.

Az eloszlásfüggvény minden folytonos véletlen változó mindig egy szakaszos lépcsős függvény ugrik, ami akkor következik be, pont megfelel a lehetséges értékek a véletlen érték és ravnyveroyatnostyam ezeket az értékeket. Az összeg az összes ugrik a függvény értéke egy.

Mivel a számos lehetséges értékei valószínűségi változó, és csökkentsék az intervallumok között az ugrások nagyobb lesz, és maguk is ugrik - kisebb; sebességgörbével simább (ábra 5.2.5.); Véletlen változók fokozatosan közelít a folytonos érték, és annak eloszlása ​​funkció - egy folytonos függvény (ábra 5.2.6.).

A gyakorlatban, általában egy folytonos függvény a valószínűségi változó függvénye, amely folytonos minden ponton, ábrán látható. 5.2.6. Azonban lehetséges, hogy állítson össze példákat valószínűségi változók, amelynek lehetséges értékei folyamatosan töltve egy bizonyos időközönként, de amelyekre az eloszlásfüggvény nem mindig folyamatos és szakaszos izolált pont (ábra. 5.2.7).

Az ilyen véletlen értékeket úgynevezett vegyes. Példaként a vegyes értékek kárt okozhat a területen, a lerakódást cél bomba, amelynek sugara egyenlő az pusztításának R (ábra. 5.2.8).

Az értékek a véletlen változó folyamatosan pótolja 0. végezzük pozíciókban bombát I. típusú és II, van néhány véges valószínűséggel, és ezek az értékek megfelelnek az ugrások az eloszlási függvény, míg a közbenső értékek (összesen III típusú) eloszlása ​​folyamatos. Egy másik példa a vegyes valószínűségi változó - T idő üzemidő készülék a vizsgált t idő alatt. A eloszlásfüggvénye valószínűségi változó folytonos mindenütt, kivéve a ponton t.