Trigonometrikus függvények, Krugosvet enciklopédia
trigonometrikus függvények
Trigonometrikus függvények - az egyik elemi funkciókat.
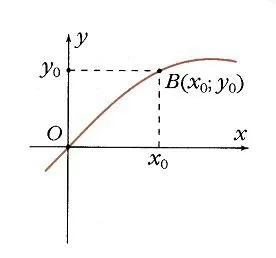
A függvény az y = cos x.
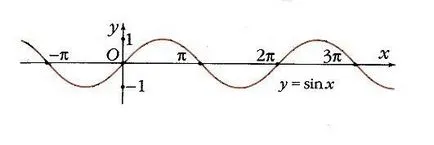
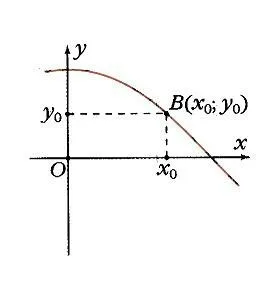
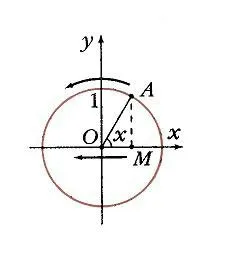
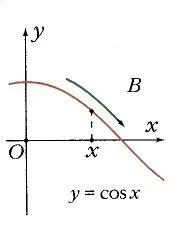
Ha össze egy egységet kört origó középpontú, és állítsa egy tetszőleges értéket az érvelés, és számolni x0 Ox szög x0, akkor ez a szög az egység kör felel meg egy A pontot (ábra. 1), és a vetítés az x-tengely egy M pont. A hossza a szegmens OM egyenlő az abszolút értéke az abszcissza A. pontja adott érték X0 van leképezve értéke függvényjel y = cos x0, mint az abszcissza A. pontban Ennek megfelelően a B pont (X0; y0) tartozik a függvény grafikonját y = cos x (2. ábra). Ha pont az, hogy a jobb oldali y tengelyen, akkor a koszinusz pozitív, ha a bal - negatív. De minden esetben, a pont nem hagyhatja el a kört. Ezért koszinusz tartományba esik -1 és 1:
-1 = cos x = 1.
További forgási bármilyen szögben a 2 többszöröse p. Egy pont visszatér ugyanarra a helyre. Ezért, a függvény az y = cos x periodikus, a periódus értéke 2 p:
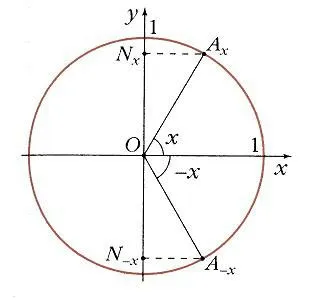
Ha veszünk két érték az az érv, egyenlő nagyságú, de ellentétes előjelű, x és -x, megtalálható a kerülete a megfelelő pontokat Ax és Ax. Amint az ábrán. 3. a nyúlvány az x-tengelyen az ugyanazon a ponton M. ezért
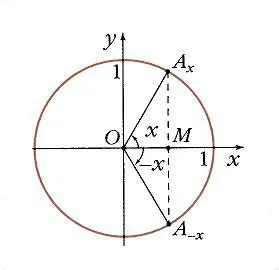
azaz koszinusz - páros függvény, F (-x) = f (x).
Ennélfogva, lehetséges, hogy vizsgálja a tulajdonságait a függvény az y = cos x a [0, p], majd a figyelembe vételére periodicitás és a paritás.
Amikor x = 0, az A pont fekszik a tengelyen Ox és abszcissza értéke 1, és így cos 0 = 1. A növekvő x pont mozog körkörösen felfelé és balra, a vetítés, természetesen, csak a bal, és amikor X = p / 2 koszinusz 0 lesz pont ezen a ponton merül fel a maximális magasságot, majd tovább halad a bal oldalon, de csökken. A abszcisszán az összes addig csökken, amíg el nem éri a legkisebb értéke egyenlő -1, amikor X = p. Így a [0, a] függvény az y = cos x monoton csökken 1-től -1 (ábra. 4, 5).
Koszinusza paritás azt jelenti, hogy az intervallum [- p. 0] függvény monoton növekszik a -1 1, feltételezve nulla érték az x = - p / 2. Ha az előírtnál több periódusban, hogy egy hullámos görbe (6.).
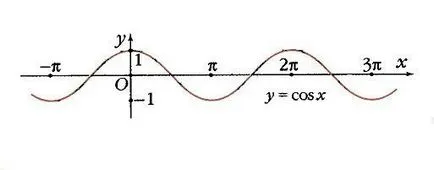
Így, az y = cos x veszi érték nullával x = p / 2 + k p, ahol k - bármilyen egész szám. Maxima egyenlő 1, vannak elért pontok X = 2k p. azaz 2. lépés p. és legalább egyenlő 1, x = p + 2k p.
A függvény az y = sin x.
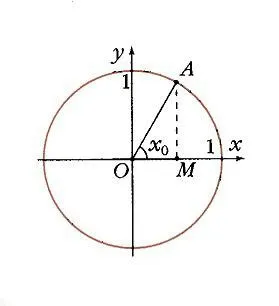
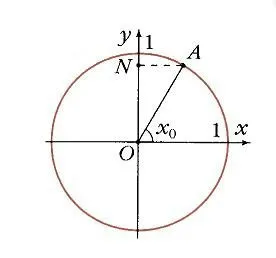
A készülék körhöz sarokban x0 megfelel az A ponthoz (ábra. 7), és annak vetülete az y-tengelyen fog mutatni N. A zár funkció W = sin X0 Y0 úgy definiáljuk, mint az ordináta az A. pontban B pont (szög x0, y0) tartozik a függvény grafikonját y = sin x (ábra. 8). Nyilvánvaló, hogy a függvény az y = sin x időszakos, időtartama egyenlő 2 p:
Két argumentum értékek X és - előrejelzések megfelelő pontokat Ax és Ax az y-tengelyen elhelyezve szimmetrikusan a ponton O. Ezért
azaz sine - páratlan függvény, F (-x) = -f (x) (9. ábra).
Ha a turn pont képest o pont a p / 2, a szög az óramutató járásával ellentétes (más szóval, ha a szög X, hogy növelje a p / 2), akkor annak ordináta pedig az új helyzetben megegyezik a régi abszcisszán. Ez azt jelenti, hogy
Egyébként sine - koszinusz van „megkésett” p / 2, mivel minden érték koszinusza „Repeat” a sinus, amikor az az érv növekszik p / 2. És annak érdekében, hogy össze egy grafikont a szinusz, koszinusz elegendően műszak ütemezés p / 2 jobbra (ábra. 10). Rendkívül fontos jellemzője fejezi ki a szinusz