A hatásfok az értékpapír-portfólió (az elmélet a Markowitz)

Ma nézzük ezt a kérdést abból a szempontból hatékony portfolió Markowitz, az első, hogy tegyen javaslatot egy olyan matematikai modellt hatékonyságának értékelésére az értékpapír-portfolió.

Még ha nem fogja használni matematikai eszköz hatékonyságának mérésére a befektetési portfólió, azt ajánlom, hogy olvassa el a cikket, hogy a végén.

Amellett, hogy a megadott képlet itt nagyon érdekes illusztrációk, amelyek képesek reflektáló és erősítik jelentős mértékben elősegíti a tudás az elmélet a beruházás ...

Nyilatkozat a problémát

Kezdjük a probléma megfogalmazása. Tegyük fel, hogy találjuk magunkat olyan helyzetben, amikor meg kell adni a biztonságot.

Tudjuk, annak költségeit (az az ár, amit megvettem), de az eladási ár nem ismert, és a mérete osztalék. ami azt várjuk, hogy megkapja az időszakra birtokában értékpapírok.

Nyilvánvaló, hogy a hatékonyságát az értékpapír értékesítéséből lesz ugyanolyan kiszámíthatatlan, mint bármely véletlen változó.

Xt jelöljük. A számértéke ez az érték lehet képlettel számítottuk ki:

Pt - az ár, amelyen a biztonsági vásárolta t időpontban,

Pt + 1 - az értékpapír árának amelyen végrehajtották a t + 1.

Várható hatékonyságát beruházások biztonságát függ a paraméter Xt.

Tény, hogy beszélünk egy függvény, amely a várakozás a támadó Xt esemény.

Jelöljük ezt a funkciót érték m, ahol m = U (X).

Kockázatok és diverzifikálása

Matematikai hatékonyságának értékelése befektetési portfolió figyelembe veszi a két fő típusa a befektetési kockázat:

[1] A rendszeres (nem akaratától függ a résztvevők a beruházási folyamat. Például politikai vagy ország kockázat),

[2] rendszertelen (kötött az egyedi befektetési eszközök, beleértve részvénytársaság, cégek, vállalkozások).

Fontos megjegyzés. Szisztematikus kockázatok nincsenek kitéve a diverzifikáció; rendszertelen, éppen ellenkezőleg, nagyon érzékenyek a diverzifikáció, valamint azért, mert még úgy is nullára csökken.

A „kockázatmentes portfólió” kifejezés jól diverzifikált portfolió, megszabadult a hatása nem szisztematikus kockázat.

Teljes körű védelmet a befektetési portfolió szisztematikus kockázatok lehetetlen.

Sajnos, riskless portfóliók gyakorlatilag nulla hozammal.

Akarva-akaratlanul, a legtöbb befektető kell, hogy átalakítsák a pénzügyi érdekek felé kockázatosabb pénzügyi eszközök biztosítása érdekében átvételét elvárt hozamát ...

Definiálása kockázati mértékek

Ezért úgy döntöttünk, hogy a hatékonyságát kiválasztott biztonsági random (a szempontból az elmélet a valószínűség) az X értéke

Ezután mérjük a kockázat ilyen nagyságrendű lesz a szórás. Ami a képletek értékmérője kockázat (variancia) felírható:

Az érték a Z mindig nagyobb vagy egyenlő, mint nulla.

Minél alacsonyabb az érték, a Z, annál kisebb a kockázat szintjét rejlő érintett mögöttes értékpapír (vagy - nincs nagy különbség - az értékpapír állomány).

Ha Z = 0, akkor kell foglalkozni a kockázatmentes portfólió.

hatékony portfóliók

Itt az ideje, hogy az érveinket jobban látható. Különösen figyeljen az alábbi ábra:

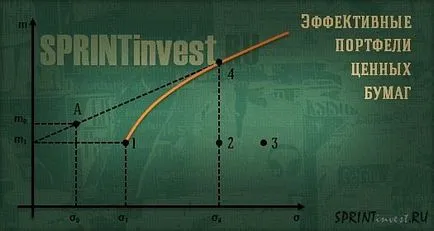
Ott vannak ábrázolva négy befektetési portfolió (1., 2., 3. és 4. ábra).

Ha a portfolió a jobb oldalon, az azt jelenti, hogy a kockázat mértéke többé. Ha az értékpapírok állománya nagyobb, így a hatékonysága is nagyobb.

Más szóval, a hatékonyságot a portfóliók 1, 2 és 3 jelentése azonos, és így alacsonyabb hatékonyságát portfolió 4.

A legkockázatosabb portfólió itt 3 és a legkisebb kockázatú portfólió jellemzi 1.

Curve narancs jelzi a határ a hatékony portfóliók.

Ez a határ képez több portfóliók, azzal jellemezve, maximális hatékonyság egy adott kockázati szint.

Szakmai befektetők hajlamosak választani a leghatékonyabb és legkevésbé kockázatos befektetési portfólió.

Esetek 1 és 4 hatásosak mint társaik a számok 2, és 3 - nem.

Minél közelebb van a befektetési portfólió, hogy a görbe jelzi határait hatékony portfóliók, ezért hatásos.

Kockázatmentes értékpapír-portfolió

Egy érdekes perspektíva a portfolió értékpapírok úgynevezett zéró befektetési kockázatot (σ0), és egy előre meghatározott hatásfok (M0).

A diagramon ez az állomány megfelel az A. pontban

Ez a lista még előnyösebb a beruházó mint táskát 1, azzal jellemezve, mert kisebb a kockázata, és sokkal nagyobb a hatékonyság (hozam).

Ahhoz, hogy a formája, hogy kell venni, mint egy kockázatmentes értékpapír, és a beruházásokat a portfolió arányban 4 [σ0 / σ4] a [(σ4 - σ0) / σ4].

Hatékony portfolió Markowitz

Minden elméleti számítások fentebb már kölcsönzött az elmélet hatékonyságát az értékpapír Garri Markovitsa portfolió.

Számára tartozik a tiszteletére az első (1951), a matematikai megfogalmazása az alapvető problémát, Tumanyan agy befektetők határozzák meg a szerkezet a portfolió. ami egy bizonyos szinten megtérülési jellemzője lenne a minimális befektetési kockázatot.

Ha bízunk chart, hatékony portfolió - egy pontot, hogy a tekercsek a megfelelő görbe határán hatékony portfóliók.

Ez az ív megfelel a feltételeknek a probléma fent.

A döntés jelölt feladata részeként Markowitz elméletét, azonban megköveteli a nagy mennyiségű statisztikai adat maximális időtartamát, amelynek során a tőzsde, amely büszkélkedhet csak néhány fejlett ország a világon (USA, Németország, Franciaország, stb.) Magyarországon addig, amíg a „repül” a lista ...

Eközben a módszerek alkalmazásához cikkben meghatározott hatékonyságának értékeléséhez az értékpapír-állomány évente egyre ésszerű.