Előadás a design origami figurák

Előadás a tárgya „Matematika” a témája: „.. tervezése számok origami origami legtöbb rajongó kezd kitalálni munkájukat egy idő után először hozzá kell több mint egy.”. Letöltés ingyen és regisztráció nélkül. - átirata:

2 Akira Yoshizawa és a origami.

3

4 kulcsfontosságú jelei és szimbólumai nyilvántartásából.

6 1. Összecsukható véletlenszerűen. A sok munka került elő véletlenül. Például azt akartuk, hogy dolgozzon ki egy szép virág. Hajtogatással, mindig figyelni, hogy mi történik a jelenlegi pillanatban, hogy továbbra is hozzá, és hirtelen észreveszi, hogy a kapott munkadarab jól látható körvonalait egy állat. Ezen a ponton meg kell elfelejteni a virágot, és teljesen váltani a képet az állat, és igyekezett, hogy a munkát a végén. 2. Változtassuk meg a hagyományos számok. Az elmúlt század legnagyobb számok nézd próbaidő. Például a zsiráf állt három lábon. A négy sarkából a tér és meglehetősen egyik sarokból, hogy a fejét a másik két mellső lábak és a hátsó lábak csak egy sarokban, ő kap egy „béna zsiráf.” Persze, hogy sok rajongó volt a vágy, hogy origami figurák több realizmus, hogy a zsiráf állt mind a négy lába! 3. Hozzon létre a számok alapján alapvető formája. Korábban, a gépek és technikák dolgozó papír át közvetlenül emberről emberre. A hagyományos japán adatok ideiglenes, egyszerű és sematikus. Tipikusan, a kezdeti redők hasonlóak voltak. Az első néhány redők kialakítva egy úgynevezett alapvető alakja. Fokozatosan kialakult hagyományos alapformája „Crane”, „béka”, stb Klasszikus alapforma origami nevezték a leghíresebb modellek, amelyek ki lehet hajtogatni őket, ez olyan, mint a kite, halak, madarak és békák. Az ábrán látható, a minták ezek alapvető formák. A minta egy rács által képzett vonalak hozzáadásával a számok.

7. Az alapvető formája a „sárkány” Az alapvető formája a „hal” alapformája „Madár” Az alapvető formája a „béka”

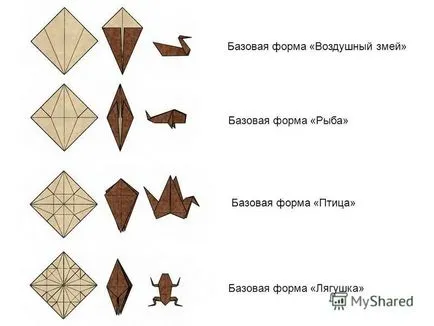
8 4. létrehozása számadatok alapján módosított bázis formában. Általában minden olyan hagyományos alapvető alakja van egy szimmetrikus szerkezetű. Ezekből a számok is, szimmetrikus. Ahhoz, hogy változtatni az arányokat számadatok szükséges átalakítása, módosítása az alapvető forma, amelyből ez származik. Sok kortárs alkotások alkalmazásával alapvető formák, kombinációk és co-location néhány alapvető formája egy lapra. Alapvető formák sok, de az átalakulás pedig elsősorban csak négy - a sárkány, halak, madarak és békák. A klasszikus példa a módosítás alapvető formája az úgynevezett „mentális vágás” a szimmetria vonalat, azzal a kiegészítéssel, a metszés a papír, hogy az előgyártmány kapott vett egy szabályos alakú, ebben az esetben a négyzet alakú. Ezzel a technikával tudjuk szerezni, például egy zsiráf. Tekintsünk egy másik példát módosítását bázikus formában. Lehetséges, hogy összekapcsolják a két teljes kész számokat az egyik? Igen, talán, de minek? Ez a művelet lehetővé teszi, hogy még valósághűbb munkát, mint korábban volt az átkelés. Például, van egy sárkány, akinek a feje dolgozott nagyon feltételes, és külön-külön reális fej, amely több részből áll. Ha tegye a fejét a szimmetria vonalat, és így válassza ki a megfelelő méretű neki, hozzátéve négyszögletes szegmensek, amelyek együtt képezné a helyes alak, négyzet, akkor egy sárkány egy fejjel.

9 kivetése két alapvető formája „Hal” feszített bázis „Madarak” palacsinta bázis „Madarak” módosított bázis „Madarak”

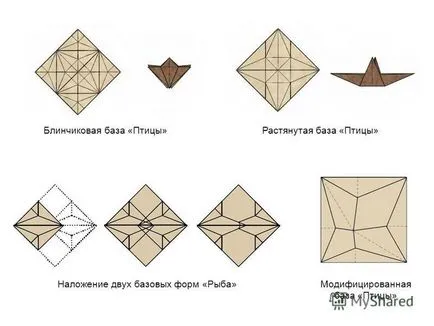
10

A fej 11 Kunihiko Kasahara + Sárkány Sárkány Sárkány Roberta Nila = Kasahara-nílusi (KNL Sárkány)

15 6. tervezése a modern technikákat. Modern origami egy klasszikus origami plusz matematika és a geometria. Modern origami elősegíti az úgynevezett tudatos kreativitás. Ha mielőtt a papír hajtogatás, nem tudjuk biztosan megjósolni a kimenetelét a munkánkat. Számos kezdeményezés nem vezettek a kívánt eredményt. Most a létrehozásának folyamatát egy új szám drámaian megváltozott. Ha telepíteni, például daru az eredeti négyzet, akkor látni fogjuk, a munkalapon rácsvonalak eredményeként jött létre az adagolás. Ez a minta az úgynevezett mintát. Bármely modell lehet telepíteni, és hogy a minta. Ennek megfelelően, ha haladunk a konkrét eljárást tervezni kívánt minta számunkra, és adjunk hozzá saját vonalak, az eredmény ez a szám, és szerettünk volna létrehozni. Kezdeni tervezésekor a mintát, meg kell kevés elméleti ismeretek a matematika és a geometria.

16 Alapvető tételek tervezéshez szükséges. 1) A1 + A2 + A3 = b1 + b2 + b3 =) száma hegyek és völgyek, származó egy pont két különböző, és mindig megegyezik páros szám. 3) olyan háromszög van hajtva mentén szögfelezői annak szögek és merőleges egyik oldalára, áthaladva metszi a szögfelező ad lapos alakú. Ezek tételek csak akkor érvényesek, lapos formákat.

17 Láthatjuk, hogy a gyakorlatban elég nehéz építeni, és kiszámítja a szögek, a minta létrehozásához. Ha építeni ezek a szögek vonalzó szögmérő, az elkerülhetetlen hibák és tévedések, amelyek felhalmozódnak, és vezet az a tény, hogy a kapott minta nem lehet elképzelni, hogy összegyűjti a szám. Az említett nehézségek elkerülése, vannak különböző tervezési technikák, amelyek közül az egyik az úgynevezett huszonkét és fél (22,5). Mint azt sejteni lehet, ha szakadék derékszögben ketté megkapjuk két szöge 45 fok. Ha egy 45 fokos ismét ketté, megkapjuk a két szög 22,5 fok. Ez a hegyesszög elegendő a kialakulását lábak, láb, és más antennák jövőbeni számok. Most nyugodtan elhagyni a vonalzó és szögmérő. A mi feladatunk az, hogy egyszerűen osztani derékszögben négy részre, és válassza ki a egyenes metszéspontja elosztjuk az így kapott pontot, hogy új csomópontot. Annak érdekében, hogy tovább hangsúlyozzák a kecses adatok, például a zsiráf, finomítását formája, szükséges, hogy felosztjuk az 45 fokos három. A kapott szög 15 fok. Erre példa a felosztás egy zsiráf Hideo Komatsu.

18 tervezési módszer 22.5

20 American Scientist matematikus, fizikus és Robert Leng origamist vizsgáló tapasztalatait papír megállapítja, hogy a teremtés a kívánt alakra egy papírlapot kell szerezni egy bizonyos számú kiálló részek különböző hosszúságú a megfelelő helyeken a munkadarabot. A kapott hegyes szegmensek nevezett fülek. A szárny egy olyan terület, a modell, hogy lehet átalakítani függetlenül más részein a modell. Annak igazolására, a design a kívánt alakú használják úgynevezett gráf vagy szárnyak fa. Vegyük például bázis formájában „madár”, és légy váltakozó külső és belső hajtások elvékonyodása füleket. Minél többet, ezek redők, a vékonyabb lesz a füleket. Ha veszünk egy nagyon vékony papír, és egy csomó ilyen ráncok, akkor a végén egy grafikont, vagy fa szárnya. Az ábrán az alapformák és szórólapok fa. A design a tervezett számok, meg kell, hogy a megfelelő mennyiségű szárnyak bizonyos hosszúságú. Vegyünk egy papírlapot, és hajtsa félbe, majd ismét felére. Most hajlítsa az átlós, és újra az átlós, amint az ábrán látható. Kapunk egy hegyes szegmensben. Fellázadt a csúcs van szükség a távolság és a humusz ugyanazon a helyen, így vázolja a szükséges hosszúsága a fedelet. Most telepíteni a papírt. Látni fogjuk körbe. A sugár lesz a hosszú szárny. Ezt a módszert nevezik a módszert körök (kör csomagolás).

21 falevelek. Graf.

23. Kiderül, hogy a teremtés számadatok kell építeni egy fa szárnyak (Earl), tegyük egy papírlapra szükséges számú köröket sugarak hosszának felel meg a mi grafikon, hogy mintát, és hajtsa. Felmerül a kérdés - hogyan tegyük egy kört egy darab papírt? A kör közepén lehet a sarokban a papír, mint az elhelyezés tekinthető a legoptimálisabb, mivel lehetővé teszi, hogy hozzon létre egy lebeny a legkisebb mennyiségű papírt. A kör közepén lehet szélén található a lap és a lap, de nem haladja meg a határait lapot. Ha a gráf szegmensek található egy pontot, akkor a megfelelő kört érintik egymást. Amikor a grafikon sokaságát tartalmazza elemek kapcsolódnak egymáshoz, akkor a csoport lesz osztva kerületük úgynevezett „folyó”. A szélessége a „folyó” felel meg a távolságot ezen elemek között. „River” mindig „folyik” a papír szélei között. De vannak kivételek. „River” lehet „flow” közvetlenül vagy kanyarog, mint egy igazi folyó. Aki szereti a matematikai tudja, hogy a feladat körök négyzetes elrendezésben az egyik kedvenc feladatai matematikus. Sok megoldást ezekre a problémákra, így matematikailag pontos leírását a megállapodás a folyamat a téren. Hála a matematika lehetővé vált, hogy írjon speciális programokat az ilyen feladatokat.

24

25 N - körök száma, R - a sugara a körök.

26 Robert Lang írt számítógépes program kialakítása, amely lehetővé teszi, hogy szerezzen egy mintát, és azt mutatja, hogy a modell fog kinézni, ha összegyűjti a minta sorokat. A program neve Treemaker. Vegyük például gyík. Látjuk, hogy van egy farok, négy lába és egy kis fej. Leadása gyík lehet sematikusan az úgynevezett csontváz vagy nyelvét beszélő tudomány grafikon. Gondoskodjon a megfelelő kerületi hosszúságú szerint a grafikon. Végezzük egyes műveletek Treemaker programot és szerezzen egy mintát. Hajtsa, megkapjuk a szükséges számú szárnyak megfelelő hosszúságú. Továbbra is, hogy a végleges formáját a munkadarab és a gyík kész! Rajzoláshoz és a vizsgálati minták léteznek Oripa program, amely lehetővé teszi, hogy dolgozzon, és putters tudja mutatni ezt a mintát a hajtogatott modell, és ez azt mutatja, egy hiba a mintát. Most mindenki néhány perc alatt lehet tervezni bármely tárgy vagy figura. Felmerül a kérdés - tehát a modern origami nem művészet, és száraz matematika? Tervezés tud valaki érti ezt a programot, az a személy? Természetesen nem. Tervezhet, és hozzanak létre egy egyszerű összehajtható és megértése nagyon összetett feladat, és az úgynevezett optimalizálás. Előfordul, hogy a folyamat optimalizálása késett sokáig, és nem az, amit a számítógépek nem tud személyesen.

29 Jelenleg az lett nagyon népszerű módszer tervezése doboz pliting. Bár ez a módszer óta ismert a múlt században. Módszer neve származik az angol - box. Az a tény, hogy számos, a dobozok hajtogatással egyetlen üres. Ez a módszer magában foglalja a meghajlás a papír csak merőlegesen és egy 45 fokos szögben. A módszer könnyen elsajátítható, elég egyszerű, és a modell tervezett vele, meg nagyon lenyűgöző. körök módszer könnyen átalakul doboz pliting. Ahelyett, hogy úgy van elrendezve, a kerülete mentén a lap, mi lesz négyzetek. Elhelyezünk egy kört a téren nem matematikai számítások meglehetősen nehéz feladat. És intézkedik négyzet egy négyzet alakú papírlapra nagyon egyszerű, és nem igényel matematikai számítások. Ezért doboz pliting ma széles körben elterjedt az egész világon. A módszer egyszerű és hatékony. Alkalmazásával kapott ez a módszer nagyon kifejező számok és reális. Box pliting kombinálható mód szerint a körök és a nagy bázis formák. Gyártunk például egy madár, hosszú lábak és ujjak. Készítünk egy grafikont. Ennek alapján vesszük az alapvető formája a „madár”, és tedd a sarokban a tuskó. Van egy csoport öt kapcsolatos körökben. Két csoport négy kört szélén a munkadarab, akkor ujjait. Kisasszony két „stream” a lábujjak, hogy a test, a „madár”. A váltakozó külső és belső redők a vékony lábak. Gyűjtjük a kapott mintát, és kap egy madár - szörnyeteg

30 Box pliting. Ökölvívó-pliting kombinált módszerével körök. Részletek szárnyakat az eljárás körök és módszer box pliting.

33 módosítása a fedelet.