Futott töltött részecskék számít
Kölcsönhatása könnyű töltött részecskék a közeggel
Mivel a kis mérete a tömegek, e ± mozog az ügy nem egy egyenes vonal, és ezek elengedhetetlenek a sugárzási energia veszteség (bremsstrahlung).
Amikor stolknoveniyahe-elektronok anyagot kell vizsgálni a metabolikus kölcsönhatását effekty.Obmennoe - kölcsönhatása azonos részecskék a kvantummechanikában, ami a függőség a részecske energiája a rendszer a teljes spin. Tisztán kvantum hatás eltűnik, ha a határérték a klasszikus mechanika.
Ionizációs fényveszteség töltött részecskék elektronok.
Passage elektronok révén anyagától eltérő anyagból áthaladását a nehéz töltött részecskék. A fő ok - egy kis elektron tömege. Ez vezet egy viszonylag nagy változás a elektron impulzust annak minden egyes ütközés részecskék a közeg, ami érezhető változás irányába elektron mozgás, és ennek eredményeként - az elektromágneses sugárzást. A fajlagos energia veszteség elektronok mozgási energiával
Ezek összege az ionizációs sugárzás és veszteségeket.
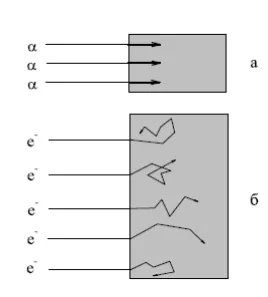
Ionizációs energiaveszteség elektronokat. Alacsony elektron energia (E <1 МэВ) определяющий вклад в потери энергии дают неупругие ионизационные процессы взаимодействия с атомными электронами, включающие ионизацию атомов. Передаваемая в одном столкновении энергия в среднем очень мала и при движении в веществе потери складываются из очень большого числа таких малых потерь. Статистические флуктуации в ионизационных процессах ведут к разбросу потерь и величин пробегов.
A nemrelativisztikus régióban ionizációs veszteségek gyorsan csökkennek növekvő energia, és eléri a minimális energiával, 1,5 MeV, E, ábra.
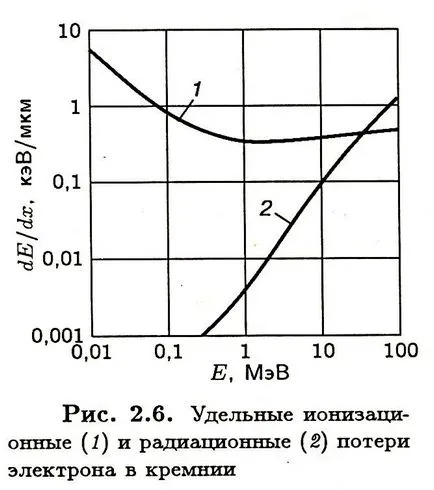
Ábra. Specifikus ionizációs (1), és a sugárzás (2) által az elektron energia veszteség szilícium
További veszteség nagyon lassan (logaritmikus) növeli az energia, platót ér el. Ennek az az oka függőség a polarizáció a tompított elektronok közepes (sűrűségű hatás). Ennek eredményeként, a Coulomb-mező legyengített relativisztikus elektron és szilárd táptalajon (szilárd és folyékony) veszteségeket nem nőnek. A gázok a veszteség növekedése elérheti a több tíz százalékkal. Kiszámításakor a veszteséget is figyelembe vesszük, attól
mozgása mind elektronok kölcsönhatás után, és hogy a
redukált tömege a kölcsönható elektronok me / 2.
Szintén figyelembe vették quantum- mechanikai hatások identitás elektronokat.
A relatív nagysága ezen korrekciók néhány százalék. A sugárzási veszteség elektronok (bremsstrahlung később tárgyaljuk részletesen).
Származtatása a képlet az energiaveszteség ionizáció útján elektronokkal, elvben ugyanazok, mint a többi töltött részecskék. Szintén a elektronok (z = 1) úgy kapjuk meg, az arány:

De az értékek bmin és bmax kell választani másképp.
Meg kell jegyezni, hogy
1) a beeső elektronok a reakció során, mert a kis mérete
a tömege lesz eltérített az eredeti irányban;
2), mert a személyazonosságát a kölcsönható részecskék fog bekövetkezni
csere hatások egy kvantum jellegű.
Ha figyelembe vesszük ezeket a megjegyzéseket, a képlet az adott ionizációs
elektron elvesztése formáját ölti:
.
Ebben a képletben
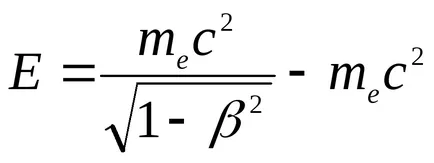
A nerelyativistskomsluchae képlet redukáljuk egy egyszerűbb kifejezést:
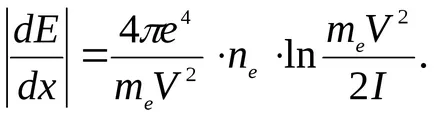
A ultrarelyativistskomsluchae PRIE »mec2 képlet az energiaveszteség is van egy egyszerű űrlap:
Ellentétben a nehéz részecskék számára egyaránt fontos ezeket az elektronokat korlátozó esetekben, mivel MEC 2 = 0,511 MeV elektron és válik ultra-, akár több MeV.
Összehasonlítás ionizációs veszteséget az elektronok és nehéz töltött részecskék vezet a következő következtetéseket.
Multipliers elülső rögzítő a kifejezéseket az ionizációs elektron elvesztése és nehéz töltött részecskék azonosak (akár a faktor 2). azaz amely azonos sebességgel sajátos veszteségek azonos (akár a faktor 2).
Bethe-Bloch képletű nehéz töltésű részecskék
Nagyon nagy energiákat, minden más. Ha V
c tagja az első konzol nem változik. Ez lesz jelentős függőség
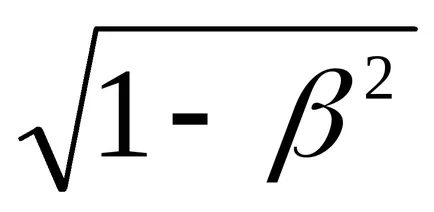
Miután elvesztette az összes energia, a részecske megáll. A megtett távolság által a részecske az anyag, ezen az úton az úgynevezett probegom.Na töltött részecske megváltoztatja energia E0 a kezdeti érték nullára eredményeként különböző interakciós mechanizmusok, a fő
amely az energia akár 100 MeV ionizációs veszteséget. Ezért nyilvánvaló, hogy a futás értéket függ a tömeg, töltés, az energia a részecske és a közeg jellemzőit.
Run R részecskék kezdeti energia E0 lehet meghatározni az expressziós
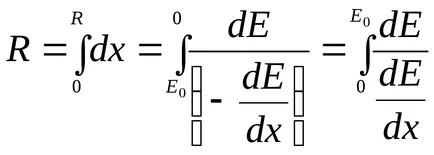

Behelyettesítve a kifejezés a nem-relativisztikus részecskék dEdlya

Most felmérni, hogy milyen távon függ a részecske paraméterek és a környezet
A következtetések ebből kapcsolatban:
1. Amikor egyenlő fut részecskesebességeket közvetlenül arányos
tömegek és fordítottan arányos a tér a díjat.
2.Probegi fordítottan arányos a közeg sűrűsége. azaz fut kényelmesen mérhető tömegegység hosszúságú. Ebben az esetben, a nagysága távon gyakorlatilag nem függ a jellemzői a közeg:
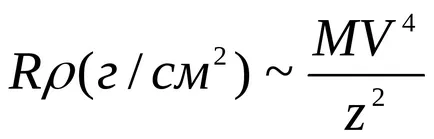
Ha pontosabb számításokat nem szabad elfelejteni, hogy a Bethe-Bloch formula több együtthatót a környezettől függően: Z / A Andi. De a legtöbb anyag az alacsony és közepes értékű otnosheniyaZ A / A
0,5, és nagyon lassan csökken a növekvő A, és az átlagos ionizációs potentsialI a logaritmusa, vagyis a is csekély hatása van az érték az átlagos teljesítmény veszteség, és ennek következtében a futás értéket.
3. Összehasonlítani a tartományok a részecskék az azonos kinetikus energia, sokkal kényelmesebb, hogy átalakítsa a kifejezés R:
Ebből az összefüggésben az is látható, hogy azonos kinetikus energiával részecskék fut fordítottan arányos a tömegek. Ez a tény ábrán mutatjuk be.
Ábra. Fut ionizációs veszteség
töltött részecskék a szilícium részecskék szilícium
Összehasonlításképpen, a grafikonok mellett ionizációs veszteséget.

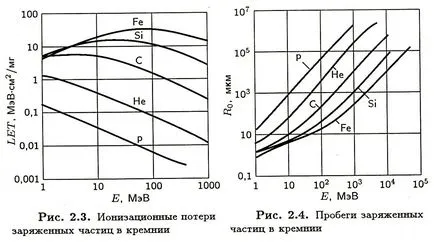
Érdekes, hogy egy empirikus viszony a pálya és energia nukleáris részecskék állíthatók elő a becsült ionizációs veszteséget:

Példaként, ábra. b mutatja kiszámítani ezt az összefüggést lineáris energiaveszteséget ugyanolyan körülmények között, mint az ábrán bemutatott adatokat. a.
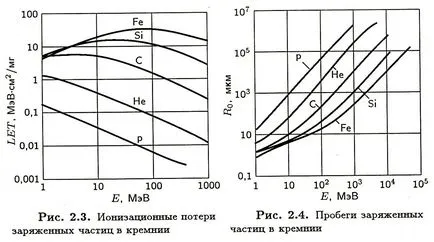
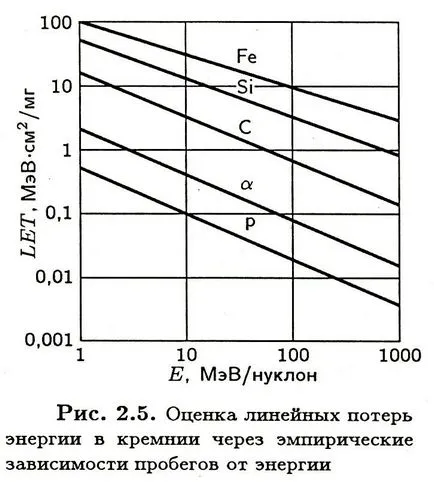
Ábra. a. Ionizációs veszteségek Ris.b. Selejtező lineáris energiaveszteség
töltött részecskék a szilícium szilícium empirikus összefüggések
fut az energia
Eredményeinek összehasonlítása azt mutatja, hogy az empirikus összefüggések olyan nagy pontossággal, viszonylag alacsony energia és a viszonylag nehéz ionok, így e kapcsolatok csak akkor lehetséges, viszonylag könnyű részecskék, és egy olyan területen, ahol van egy monoton csökkenő függés LET energia a részecske.