Összefoglaló modális szabályozás és annak előnyeit
Előadás: modális vezérlő
A lényege modális kontroll, hogy meghatározza a numerikus értékek a transzfer együtthatók valamennyi szabadonfutó üzemi állapot változókat az objektum biztosítása érdekében egy előre meghatározott eloszlását a gyökerek a karakterisztikus egyenlet a zárt ACS.
SAU karakterisztikus egyenlet teljesen meghatározza annak szabad mozgását

minden egyes alkatrész
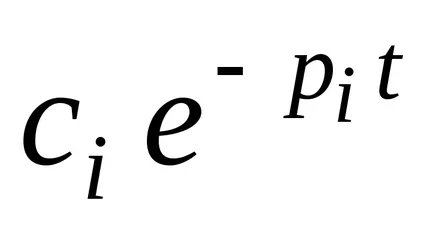
A szakirodalom nyújt a különböző szabványos készlet jellemző polinomok 1-8 megrendelések és megfelelő grafikus tranziensek rájuk az említett minőségi mutatók (binomiális Newton polinomok, polinomok Butterworth és munkatársai.). Alapján a sorrendben a tárgy és a minőségi mutatók a leírásban definiált ACS, tervező dönthet úgy, hogy a menetrend a kért átmenet és a megfelelő „normál” karakterisztikus polinomja, majd segítségével kifejtett továbbiakban algoritmus elvégzésére szintézis modális OS biztosító, előre meghatározott minőségi mutatók ACS. Így, modális szabályozás elmélet lehetővé teszi a szintézis több-a hurok zárt ACS az előre meghatározott minőségi mutatókat.
Innen kövesse a négy legfontosabb előnye modális szabályozás:
1. A szintetizált modális ACS nem igényel ellenőrzése a stabilitás (ahogy azt az előre stabilnak kell lennie, és hogy rendelkezik a szükséges mértékű stabilitás).
2. A szintetizált modális ACS nem igényel bevezetése további korrekciós készülékek (mivel ő már megfelel az előírt minőségi mutatók).
3. Bevezetés a modális operációs rendszer, köszönhetően a tehetetlenség-mentes, nem növeli az, hogy a tárgy, és nem sérti az irányíthatóság és megfigyelhetőség (amely gyakran szuper-
ötödik beadása után észlelhető passzív inerciális korrekciós eszközök).
4. A viszonylagos egyszerűsége és a gazdaság technikai végrehajtás modális ACS (mivel a modális OS végrehajtás alkalmazásával lehet végezni egy alacsony teljesítmény mérése és a konverziós eszközök és az elektronikus erősítők kis hőveszteség).
A szintézisét egydimenziós modális szabályozók.
Nyilatkozat a problémát. Egyenlet adja meg teljes kezelt objektum egy bemenet:
ahol
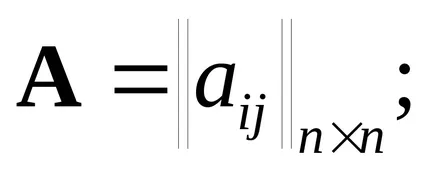
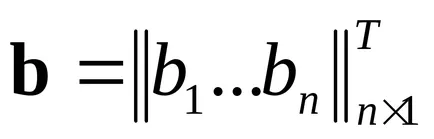
Ez szükséges, hogy meghatározzuk az átviteli együtthatók
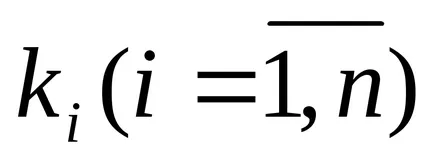
amelyben egy zárt automatikus ellenőrző rendszer volna a kívánt „standard” karakterisztikus polinom
Megoldás alapja a használata a következő tétel: Legyen a mátrix teljesen szabályozott rendszer áll rendelkezésre két különböző bázisok
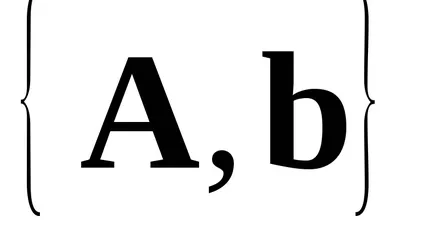
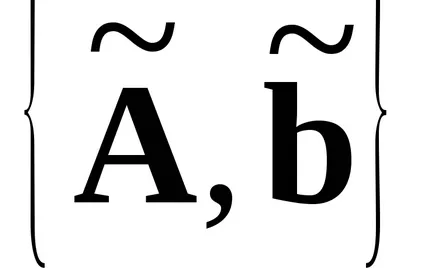
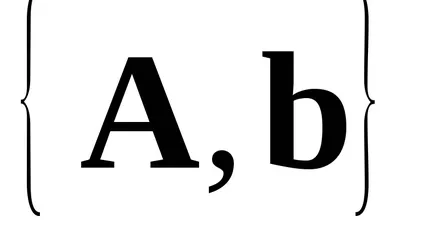
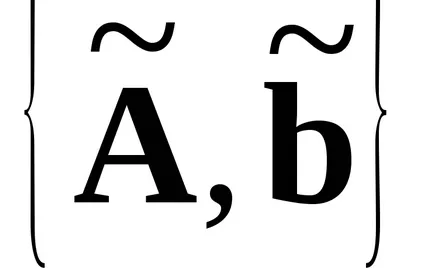
Alapján (1), (2) levelet az egyenlet a mozgás szabad zárt SAU
Mi határozza meg a karakterisztikus polinomja A mátrix:
Írja a megfelelő pár

(Ez a forma az írás az úgynevezett normál forma).
Most szerint (6), (5) és (4) ki tudjuk számítani a mátrix P kanonikus transzformáció tárgy és levelet az egyenlet (1) a kanonikus formában


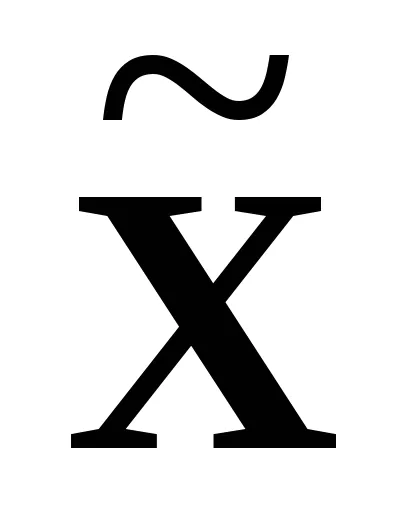

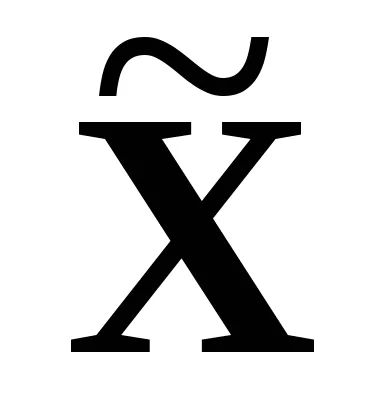
így természetesen mátrix