Pont tartozik a szegmens, geometriai algoritmusok, programmirovanie-DLA-sshool
Olvasmány a sorozat „Geometriai algoritmusok”
Szia, kedves olvasó!
Ma megnézzük egy másik tipikus feladata egy sor geometriai algoritmusok. Írj egy függvényt, amely ellenőrzi a hovatartozását bármely pontján a szegmensben. mivel a koordinátáit kezdetét és végét.
Megvalósítása összehasonlítások a valós adatok levelet még két funkciója van: EqPoint () függvény, amely ellenőrzi, hogy a két pont egybeesik a gépen, és a funkció RealMoreEq (). amelyet használni, hogy ellenőrizze a kapcsolat „> =” (nagyobb vagy egyenlő). Ennek oka az, belépő speciális funkciók már tudjuk.
Feladat. Ellenőrizze, hogy a pont tartozik a szegmensben.
Hagyja, hogy a pontokat - a kezdő- és végpontját a szegmens. - tetszőleges pontot a síkon.
Egy vektor, kezdve a pont és a végpont lesz koordinátái (x2-x1, Y2-Y1).
Ha P (x, y) - tetszőleges pont, a koordinátáit a vektor egyenlő: (x-x1, y - y1).
A P pont fog tartozni a szegmenst, ha:
- Vektorok és egy egyenesbe esik (nulla a vektor termék):
. azaz (X-x1) (y2-y1) - (y-y1) (x2-x1) = 0 - Az abszcisszán a P pont kielégíti állapot vagy. Ellenkező esetben a pont lesz a sor, hogy a bal vagy a jobb hosszát.
Az eredményeket a program.
Adja meg a pontok koordinátáinak: x1, y1, x2, y2, x, y
0.5 1 2.5 2.8 1.203 1.633
Igen.
Vizsgálati eredmények a program GeoGebra:
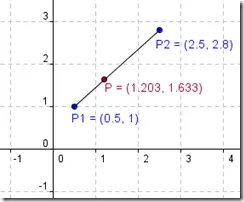
Ma írtunk AtOtres () függvényt. hogy a vizsgálatokat egy tetszőleges ponton tartozó szegmens, mivel a koordinátákat.
Bevezetett két kiegészítő funkciók: EqPoint () és RealMoreEq (), hogy végre az összehasonlításokat valós adatokat. Az először ellenőrzi, hogy a két pont ugyanazon a síkon, és a második - használják, hogy teszteljék a kapcsolat „> =”.
A következő lecke alapján korábban írt eljárások, írja a meghatározására irányuló eljárást koordinátáit metszéspontja két szegmensben.
Ezzel búcsúzom neked. Találkozunk a következő leckét.
Oszd meg barátaiddal
Köszönjük a képlet!
Jó napot kívánok. Köszönöm. nagy segítség a leckét, de van egy kérdés. Azt jelezték, hogy colinearity a vektorok kell kielégíteni az egyenlet (x-x1) (y2-y1) - (y-y1) (x2-x1) = 0 yavlyaetsya vektor termék. Nem értem ezt a pontot. A vektor termék egy vektor. A keresés a fenti egyenlet, jól értem egyenlet származó egyenes áthaladó két pontot a síkban (X-x1) / (x2-x1) = (y-y1) / (y2-y1). Javíts ki, kérlek, ha tévedek, de nekem úgy tűnik, hogy a hiba itt.
- közötti szög a vektorok, P1P2 és P1P = 0, ugyanazt a számára P2P1 és P2P. Alternatív módon, a sebesség, a belső termék ezen vektorok> = 0, mert A tényleges értékek a szögei nem kell.
Az oldal jön létre a diákok és a tanárok informatikai. A honlapon megtalálható órák programozási nyelvek Pascal, Lazarus és a Visual Basic.NET.
Ezen kívül, itt meg fogja találni órák 3-D modellező program Blender.