WolframAlpha orosz mátrix módszer megoldására rendszerek lineáris algebrai egyenletek
Mátrix módszer megoldására rendszerek lineáris algebrai egyenletek
Kérdés megoldani. amelyet korábban alkalmazott. az oldat előállítása egy lineáris algebrai egyenletek (SLAR) a Wolfram | Alpha, sőt, egy univerzális kérelmet az egyenletek megoldása és azok rendszereinek Wolfram | Alpha. Tulajdonképpen megoldására egy lineáris algebrai egyenletek ez csak, ha a rendszer úgy van beállítva, hogy természetes úton: a megkeresést követő megoldja egyenletek a rendszer fel van sorolva, vesszővel elválasztva. Ez a módszer jó, mert lehetővé teszi számunkra, hogy megoldja nemcsak bizonyos, hanem bizonytalan rendszer - általánosságban.
Annak érdekében, hogy megoldják az egyes rendszerek lineáris algebrai egyenletek is használják mátrix módszer.
A Wolfram | Alpha megoldására rendszerek lineáris algebrai egyenletek mátrix módszer egy speciális LinearSolve kérelmet. majd a mátrix együtthatók a vektor (oszlop mátrix) ingyenes tagok.
Ahhoz, hogy megértsük a funkciók LinearSolve lekérdezés szintaxist. tanulmányozza a következő példák.
Kezdeni, úgy véljük, a megoldás a homogén rendszerek lineáris algebrai egyenletek. Kérésre LinearSolve be a mátrix együtthatók a rendszer, és a nulla vektor szabad feltételeket. kapjuk:
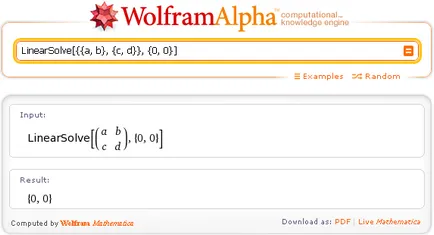
Itt Wolfram | Alpha ad triviális megoldás.
Hasonlóképpen könnyen Wolfram | Alpha úgy triviális megoldás homogén rendszerek lineáris algebrai egyenletek magasabb dimenzióban.

Most nézd meg a megoldást inhomogén rendszerek lineáris algebrai egyenletek.
Miután a kérelmet LinearSolve bevezetni a mátrix koefficiensek és egy nem nulla vektor ingyenes tagok. Válaszul a vektor kinyerésére az ismeretlenek. Íme két példa.

