játékelmélet
Játékelmélet. A döntési mátrix játék, például.
A játék meg a fizetési mátrixban. Meghatározni az optimális stratégiát számít, az első stratégia geometriailag, és a második stratégia - a szimplex módszer.
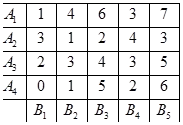
megoldás:
Megtudja, ha van nyereg pont.
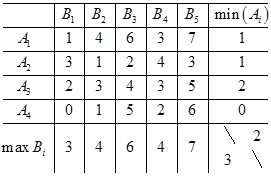
Az alacsonyabb érték a játék
A legmagasabb árat a játék
mert Az alacsonyabb ár nem egyezik meg a legmagasabb árat, akkor nincs nyereg pont, azaz a döntési mátrix játék meg kell keresni a kevert stratégiák.
Megvizsgáljuk a mátrix szempontjából dominanciáját.
Stratégia dominál stratégia, mivel minden elemét az ötödik oszlopban nagyobb, mint a megfelelő elemek a második oszlopban. Távolítsuk el az ötödik oszlopban.
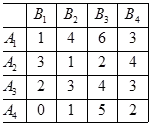
Stratégia dominál stratégia.
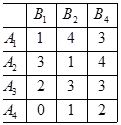
Stratégia dominál stratégia.
A stratégia szigorúan dominált stratégia.
Az így kapott mátrixot nyer, ahol a játékosok az A és B nincs domináns stratégia.
Először is, azt látjuk, a játékos B. Vegyük észre, hogy oldja meg a következő lineáris programozás feladata optimális stratégiát:
Minimalizálása a funkció figyelemmel a korlátok:
mert csak két változót, akkor ez a lineáris programozási feladat a legegyszerűbb módja, hogy megoldja grafikusan. Építünk a készlet lehetséges megoldásokat, azaz területen, amelyet ezek az egyenlőtlenségek és határolja a következő sorokat:
Szerint az x-tengely késni fog. és a függőleges tengelyen. FIELD megengedett érték árnyékos sárga.
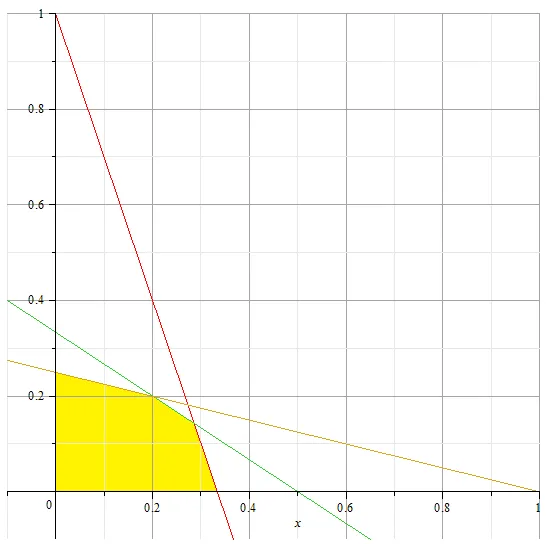
Épület egy szintig. amelyek az űrlapot. ahol C - egy tetszőleges konstans. Tisztában vagyunk azzal, hogy annak érdekében, hogy növelje a C sort kell elfoglalni a legtöbb „nagy” helyzet, de mivel a terület megvalósítható megoldásokat legalább egy pontot.
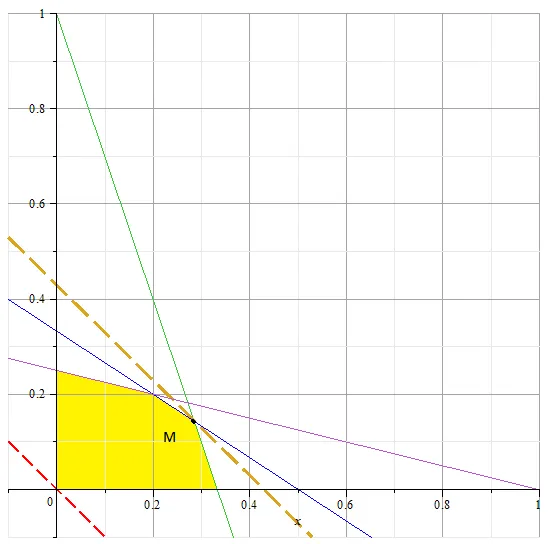
Egy ilyen helyzetben a sor - ponton áthaladó M. Keressük annak koordinátáit a két egyenes metszéspontját.
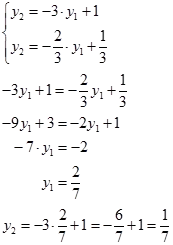
Kaptunk. majd
és